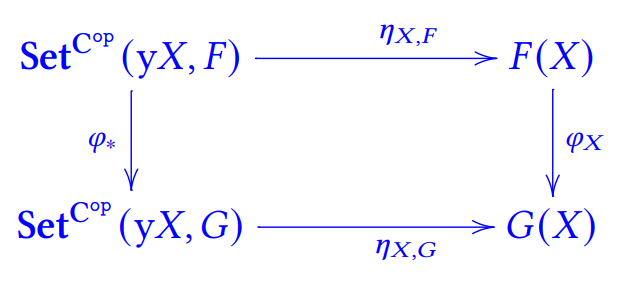理解,理解,还是要理解。
我们考虑定义一个 Yoneda Functor: y:C→SetCop。给定一个X∈C,那么yX 就是一个Cop→Set 的 functor,定义如下:
yX(YfZ)=C(Y,X)λg.g∘fC(Z,X)
那么对于XfY 是C 中的一个 morphism 的话,yX⇒yY 应该就是一个 natural transformation。
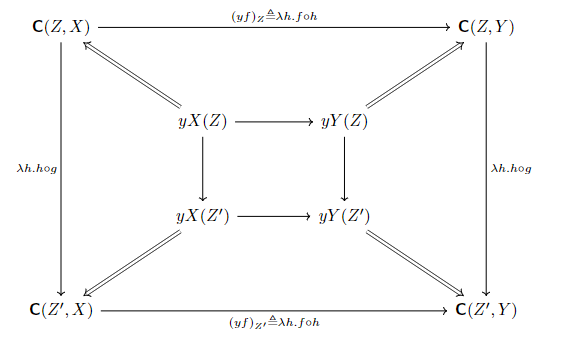
对于ZgZ′∈Cop:
![1]()
Yoneda Lemma: For each small category C, each object X∈C and each presheaf F∈SetCop, there is a bijection of sets:
ηX,F:SetCop(yX,F)≅F(X)
which is natural in both X and F.
注意,yX,F:Cop→Set 都是 functor,而SetCop(yX,F) 就是这两个 functor 之间的 natural transformation 的集合。而这个集合同构于F(X)。
下面我们试图给出这个同构映射,证明该引理。
给定一个θ:yX⇒F,那么有θX:yX(X)→F(X),因为yX(X)=C(X,X),所以θX(idX)∈F(X)。
那么我们可以定义,ηX,F(θ)≜θX(idX)。
反之,对于任意x∈F(X),Y∈C 和态射f∈C(Y,X)=yX(Y),有:
F(X)F(f)F(Y)∈Set
因此,F(X)(x)∈F(Y)。
我们定义的ηX,F−1 应该是给定一个x∈F(X),返回一个yX⇒F 的 natural transformation。即我们定义:
(ηX,F−1(x))Y:yX(Y)→F(Y)=C(Y,X)→F(Y)
我们定义
(ηX,F−1(x))Y≜λf.F(f)(x)
接下来,我们证明ηX,F∘ηX,F−1=idF(X):
ηX,F(ηX,F−1(x))=(ηX,F−1(x))X(idX)=(λf.F(f)(x))(idX)=F(idX)(x)=idF(X)(x)=x
要证明ηX,F−1∘ηX,F=idSetCop(yX,F) 即:
(ηX,F−1(ηX,F(θ)))=θ:yX⇒F
即证明,对于任意yXθF 和XfY,有:
(ηX,F−1(ηX,F(θ)))Yf=(ηX,F−1(θX(idX)))Yf=F(f)(θX(idX))
因为θ:yX⇒F 是一个 natural transformation,因此有:
F(f)∘θX=θY∘(λg.g∘f)
因此,
(ηX,F−1(ηX,F(θ)))Yf=F(f)(θX(idX))=θY(λg.g∘f)(idX)=θY(f)
下面我们需要证明ηX,F 对于F 是 natural 的。即给定一个X,和FφG,我们要证明下图是交换的
![2]()
注意,φ∗ 是从 natural transformation 到 natural transformation 的映射。给定一个yXθF,有C(Z,X)θZF(Z),那么:
φ∗(θ)Z:C(Z,X)→G(Z)
即φ∗(θ)Z=φZ∘θZ。(这里 naturality 体现在给了FφG 后,自然引导出的SetCop(yX,F)→SetCop(yX,G) 的函数φ∗。
要证明交换,即:
φX(ηX,F(θ))=φX(θX(idX))=(φ∘θ)X(idX)=ηX,G(φ∘θ)=ηX,G(φ∗(θ))
另一方面,要证明 natural in X,那么确定一个F 后,要证明对于任意给定的XfY,x 下图是交换的:
![3]()
给定了XfY 后,那么yX,yY 就都是Cop→Set 的 functor,而yf 就是yY⇒yX 的 natural transformation。
注意,这里为什么是yY⇒yX 的 natural transformation 呢?因为 Yoneda Functor y 是一个C→SetCop 的 functor,那么给定XfY∈C,yf 也应该是SetCop 中从yY 到yX 的 morphism,即从yY 到yX 的 natural transformation。
实际上,(yf)Z=λg.f∘g:C(Z,Y)→C(Z,X)。
给定一个F 后,既然有了yYyfyX,就可以自然地定义(yf)∗:SetCop(yX,F)→SetCop(yY,F)。
对于任意一个 natural transformation yXθF,(yf)∗(θ) 也是一个 natural transformation,即:
(yf)∗(θ)Z=θZ∘(yf)Z:C(Z,Y)→F(Z)
那么要证明上图是交换的,实际上就是对于任意一个θ,有:
F(f)(ηX,F(θ))=F(f)(θX(idX))=θY((λg.g∘f)(idX))=θY(f)=θY((yf)Y(idY))=(θ∘yf)Y(idY)=ηY,F(θ∘yf)=ηY,F(yf∗(θ))
# 理解和解释
我们重新审视以下 Yoneda Lemma 的式子,更简便地、它可以写为:
Nat(Hom(−,X),F)≅F(X)
其中,Nat(F,G) 表示从F 到G 的 natural transformation 的集合。
而Hom(−,X):Cop→Set 是一个 Functor,F 也是Cop→Set 的 Functor。其中
Hom(−,X)(YfZ)=Hom(Y,X)f∗=λg.g∘fHom(Z,X)
为了理解这个抽象的同构关系,我们先看几个引理,试图感觉一下,它实例化后的含义。
Collaroy 1. 如果F=Hom(−,Y) 也是一个Cop→Set,那么代入可以直接得到:
Hom(X,Y)≅Nat(Hom(−,X),Hom(−,Y))
这说明什么?别忘记,Nat(−,−) 是 functor category SetCop 里两个 object 之间的 morphism 集合!
实际上,我们找到了一个 embedding,把C 嵌入到了SetCop:
XHom(X,Y)↦Hom(−,X)↦Nat(Hom(−,X),Hom(−,Y))
对于SetCop 中的 object,那些形如Hom(−,X) 被称为 representable functor(即被X represent 了)
那么这个嵌入说明了一个事情:
对于任何 Representable Functor 之间的 natural transformation,都是 arise from 一个它们代表元之间的 morphism。
即对于任意 natural transformation Hom(−,X)θHom(−,Y),都存在一个 morphism XfY 和θ 对应。
给定XfY 后,很自然可以诱导出一个 natural transformation Hom(−,X)θHom(−,Y):
θZ=λg.f∘g
而这个引理说明,这个诱导是可逆的,对于任何一个 natural transformation 也只有唯一的 morphism。
Collaroy 2. X≅Y if and only if Hom(−,X)≅Hom(−,Y)。
这其实是因为,X↦Hom(−,X) 是一个 fully faithful 的 functor。
一个 functor F:C→D 被称为 fully faithful,当且仅当HomC(X,Y)≅HomD(F(X),F(Y))。
然后对于一个 fully faithful functor,有:如果F(X)≅F(Y),那么X≅Y。
这是一个很有哲学意义的引理。它说明了,object 的 property,实际上都是从它和周围 object 的 relation 中决定的。
即对于两个 object X,Y,如果我们从任意一个第三方 object Z 去观察它们(即 morphism 看作是一种观察,关系…)那么X≅Y 就当且仅当,Hom(Z,X)≅Hom(Z,Y)。
严格来说:
如果对于任意Z,Hom(Z,X)≅Hom(Z,Y),并且这个同构 natural in Z,那么就有X≅Y。
如果取个 dual category,其实Hom(X,Z)≅Hom(Y,Z) 也可以得到X≅Y。
注:考虑同构η:Hom(Z,X)≅Hom(Z,Y),那么η natural in Z 的含义是,对于任意Z1fZ2∈C,有:
Hom(f,Y)∘ηZ1=ηZ2∘Hom(f,X)
就是一个交换图。(注意,Hom(−,X) 是Cop→Set 的 functor)
我们重新回到 Yoneda Lemma 的原始形式。给定一个 object X 和一个 Functor F:Cop→Set,以及引导出的 functor Hom(−,X):Cop→Set。
什么是好得到的呢?F(X) 显然是知道的,因为F,X 都给了。
但从Hom(−,X) 到F 的 natural transformation 却是难以得知的,而且可能存在特别多的情况。
然后 Yoneda Lemma 就说明了,natural transformation 都是由F(X) 中的元素诱导出来的。