唧唧复唧唧,十日九风雨。
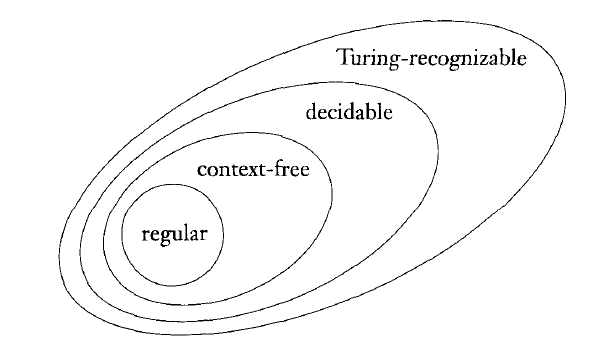
# Regular language
Language is the set of strings.
# Finite automata
Definition(Finite automaton)
A finite automaton is a 5-tuple , where
- is a finite set called the states.
- is a finite set called the alphabet.
- is the transition function. (Not partial function!)
- is the start state.
- is the set of accept states.
If is the set of all strings that machine accepts, we say that is the
language of machine and write .
We say that recognizes or that M accepts A. Because the term accept has different meanings when we refer to machines accepting strings and machines accepting languages, we prefer the
term recognize for languages in order to avoid confusion.
A machine may accept several strings, but it always recognizes only one language.
Definition(Computation)
Let be a finite automaton and let be a string where each is a member of the alphabet . Then accepts if a sequence of states in exists with three conditions:
- .
- , for .
- .
We say that recognizes language if .
Definition(Regular language)
A language is called a regular language if some finite automaton recognizes it.
Definition
Let and be languages. We define the regular operations:
-
Union:
-
Concatenation:
-
Star:
Theorem:
The class of regular languages is closed under the union operation.
Proof: Let recognize and recognize . Then we construct to recognize .
# Nondeterminism
Definition(Nondeterministic finite automata)
A nondeterministic finite automaton is a 5-tuple , where
- is a finite set called the states.
- is a finite set called the alphabet.
- is the transition function.
- is the start state.
- is the set of accept states.
Definition(Computation)
Let be a nondeterministic finite automaton and let be a string where each is a member of the alphabet . Then accepts if we can write as , where and a sequence of states exists in with three conditions:
-
.
-
, for .
-
.
Theorem:
Every nondeterministic finite automaton has an equivalent deterministic finite automaton.
Proof: Let be the NFA recognizing some language . We construct a DFA recognizing . Before doing the full construction, let’s first consider the easier case when has no arrows.
Now we need to consider the arrows. To do so we set up an extra bit of notation. For any state of we define to be the collection of states that can be reached from by going only along arrows, including the members of themselves. We need to replace by
and replace with
Example:
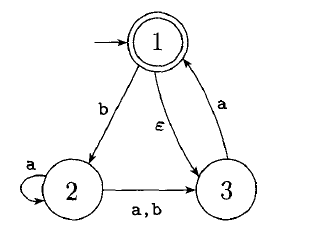
| [1,3] | [1,3] | [2] |
| [2] | [2,3] | [3] |
| [2,3] | [1,2,3] | [3] |
| [3] | [1,3] | [] |
| [1,2,3] | [1,2,3] | [2,3] |
| [] | [] | [] |
Then the DFA is
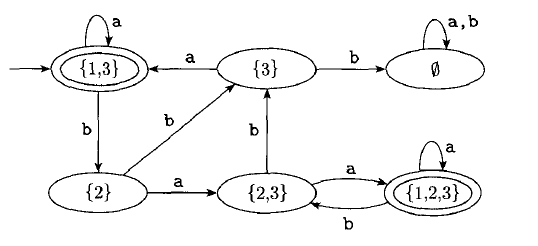
Theorem:
The class of regular languages is closed under the union operation.
Proof: since the theorem has been proved before, here we give an informal proof: given two DFAs: and , we can construct an NFA to recognize :
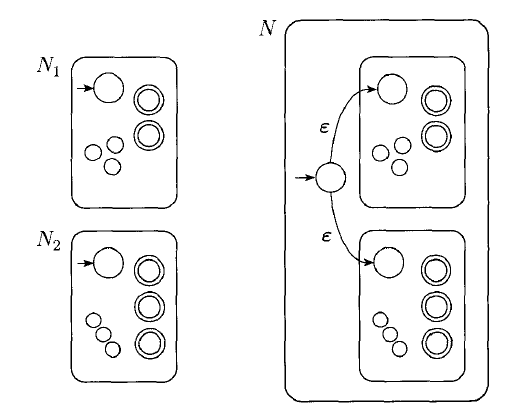
Theorem:
The class of regular languages is closed under the concatenation operation.
Proof: Suppose we are given two DFAs: and , we can construct an NFA to recognize :
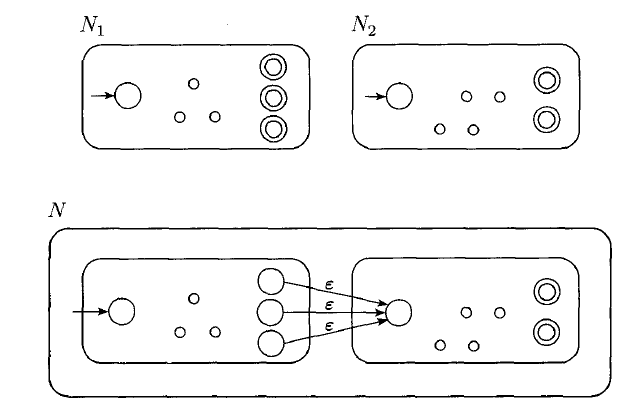
Theorem:
The class of regular languages is closed under the star operation.
Proof:
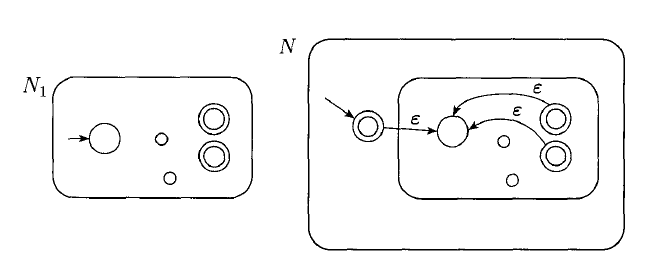
Theorem:
The class of regular languages is closed under the complement.
Proof: we can swap the accept states and other states in the DFA
Theorem:
The class of regular languages is closed under the intersection.
Proof: , since regular language is closed under union, complement, so it is closed under intersection.
# Regular expressions
Definition(regular expression)
Say that is a regular expression if is
- for some in the alphabet
- , where are regular expressions
- , where are regular expressions
- , where is regular expressions
Example:
Theorem:
A language is regular if and only if some regular expression describe it.
Proof:
One direction: If a language is described by regular expression, then it is a regular language.
We need to construct NFA to recognize corresponding regular expressions, which is the same as the proof of closure under operations.
Example: building an NFA recognizing
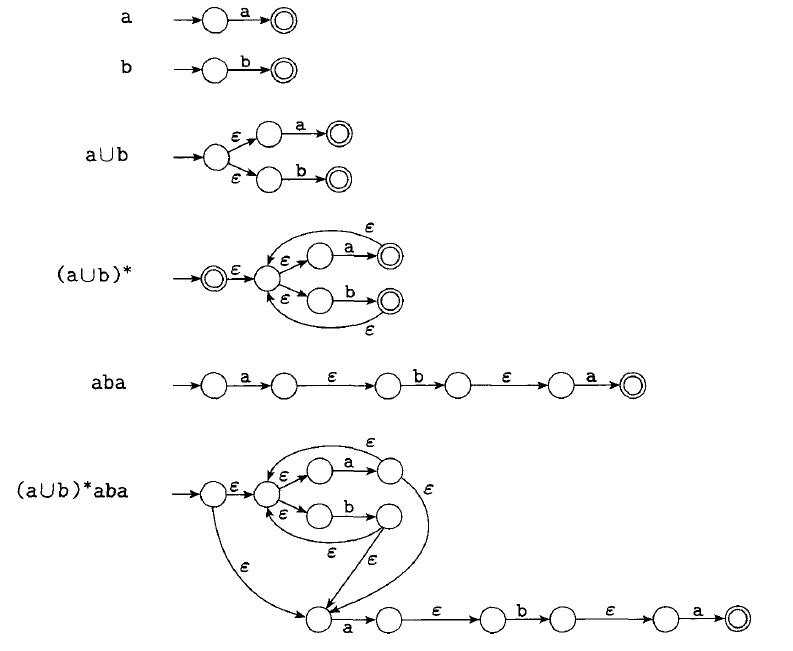
The other direction: If a language is regular, then it is described by a regular expression. I have my own method to do it. example:
- Step1. construct a new accept state, and add arrows from accept states to the new state:

- Step2. remove self-loops. If a state has a self-loop with character , then we need to add to every arrow from to other states. Specially if has no arrows from it, then you can just remove .

- Step3. remove states. If we want to remove state , then we need to enumerate all states which form following transitions:
where and are regular expressions. Then we can remove , and add arrows from to with regular expressions .
since in the example, the state 2 has only one in-arrow and only one out-arrow, so it can be removed easily. However, for those states who have in-arrows and out-arrows, we need to add new arrows.
# Nonregular languages
Theorem (Pumping Lemma)
If is a regular languages, then there is a number (the pumping length) where, if is any string in of length at least , then can be divided into three pieces, , satisfying the following conditions:
- for each , (Notice! when , )
Proof: Let be a DFA recognizing and be the number of states of M: .
Let be a string in of length , where . Let be the sequence of states that enters when processing , so .
Since , there are two states in the sequence are the same. Without loss of generality, we assume . Besides, since if , then there must be two same states in .
Then we can divide the string as
since , so after reading and , would enter the same state.
So no matter how many times repeats, always enter the same state and loop.
So can always be accepted.
Example: Consider the language . Now we can prove it’s not a regular language with pumping lemma.
Assume to the contrary that it’s regular, then there exists a pumping lemma .
However, for any , we can construct a string: , whose length is greater than and cannot be divided into three parts satisfying three conditions.
So it’s not a regular language.
# Context-free language
Definition(context-free grammar)
A context-free grammar is a 4-tuple , where
- is a finite set called the variables
- is a finite set, disjoint from , called the terminals
- is finite set of rules, with each rule being a variable and a string of variables and terminals
- is the start variable
If and are strings of variables and terminals, and is a rule of grammar, we say that yields , written /
Say that derives , written , if or if a sequence exists:
The language of grammar is .
A derivation of a string in a grammar is a leftmost derivation if at every step the leftmost remaining variable is the one replaced.
Definition
A string is derived ambiguously in context-free grammar if it has two or more different leftmost derivations. Grammar is ambiguous if it generates some string ambiguously.
Sometimes when we have the ambiguous grammar, we can construct another unambiguous grammar generating the same languages. While some ambiguous grammars cannot. We call the latter grammar inherently ambiguous.
Example: s inherently ambiguous.
Definition(Chomsky normal form)
A context-free grammar is in Chomsky normal form if every rule is of the form
where are any variables except that can’t be the start variable, and is any terminals.
In addition we permit the rule when is the start variable.
Theorem
Any context-free language is generated by a context-free grammar in Chomsky normal form.
Proof: If we have a context-free grammar, we can construct the corresponding Chomsky normal form as follows.
Example:
-
Step1, we add a new start variable and the rule , where was the original start variable.
-
Step2, we take care of all rules. We remove where is not the start variable. Then for each occurrence of an on the right side of a rule, we add a new rule with that occurrence deleted.
-
Step3, we remove unit rules :
-
Step4, we destruct rules that length
Done.
# Pushdown automata
Definition(Pushdown automaton)
A pushdown automaton is a 6-tuple , where and are all finite sets, and
-
is the set of states
-
is the input alphabet
-
is the stack alphabet
-
is the transition function
-
is the start state
-
is the set of accept states
Definition(Computation)
A pushdown automaton computes as follows. It accepts input if can be written as , where each and sequences of states and strings exists that satisfy the following three conditions:
- .
- where and .
- .
Intuitively, are the state of stacks at each position. Initially means that the stack is empty.
Example:
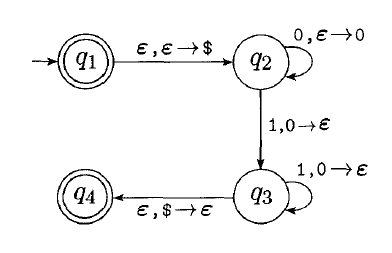
Notice that the state transition function is of the form “” which means that at state , we read character from tape, the pop character from the stack and push character into the stack. can be so we can choose not to pop/push characters.
Theorem
A language is context free if and only if some pushdown automaton recognizes it.
Proof: we can transform any CFG to pushdown automaton and any pushdown automaton to CFG.
-
One direction: from CFG to pushdown automaton. Given a CFG and an input string , we need to construct a pushdown automaton to accept if and only if the CFG can yield .
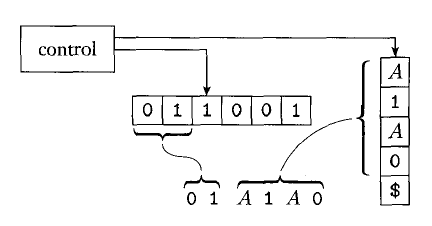
![12]()
The pushdown automaton work as follows:
- Place the marker symbol $ and the start variable on the stack,
- Repeat the following steps forever:
- If the top of stack is a variable , then nondeterministically select one of the rules for and substitute by the string on the right side of the rule.
- If the top of stack is a terminal symbol , read the next symbol from the input and compare it to . If they match, repeat. If they do not match, reject on this branch of the nondeterminism.
- If the top stack is the symbol $, enter the accept state.
We can give the algorithm:
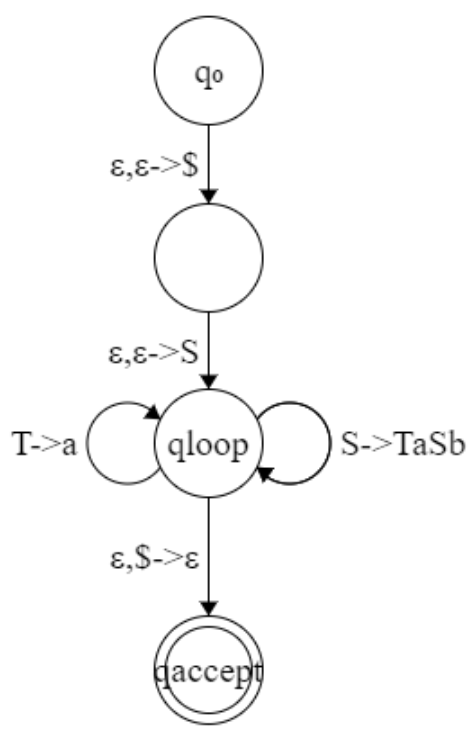
-
Construct four states as follows. And put all rules self-loop in state:
![13]()
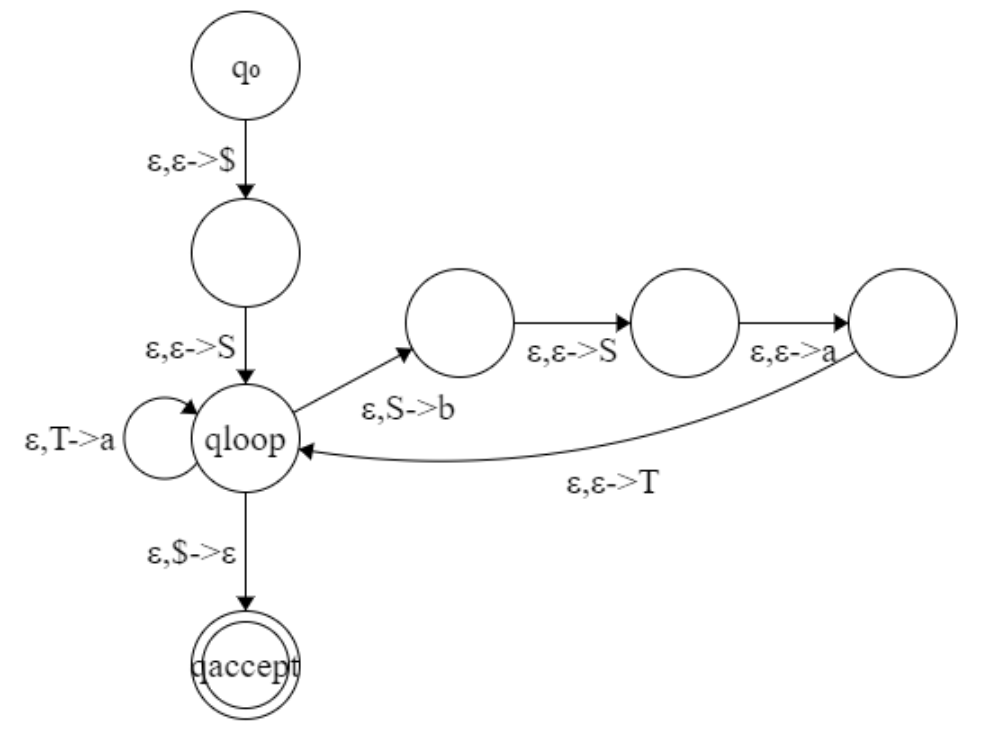
-
Destruct the derivation rules:
![14]()
In fact this step is to pop and push its derivation string. Pay attention that the string is pushed from right to left.
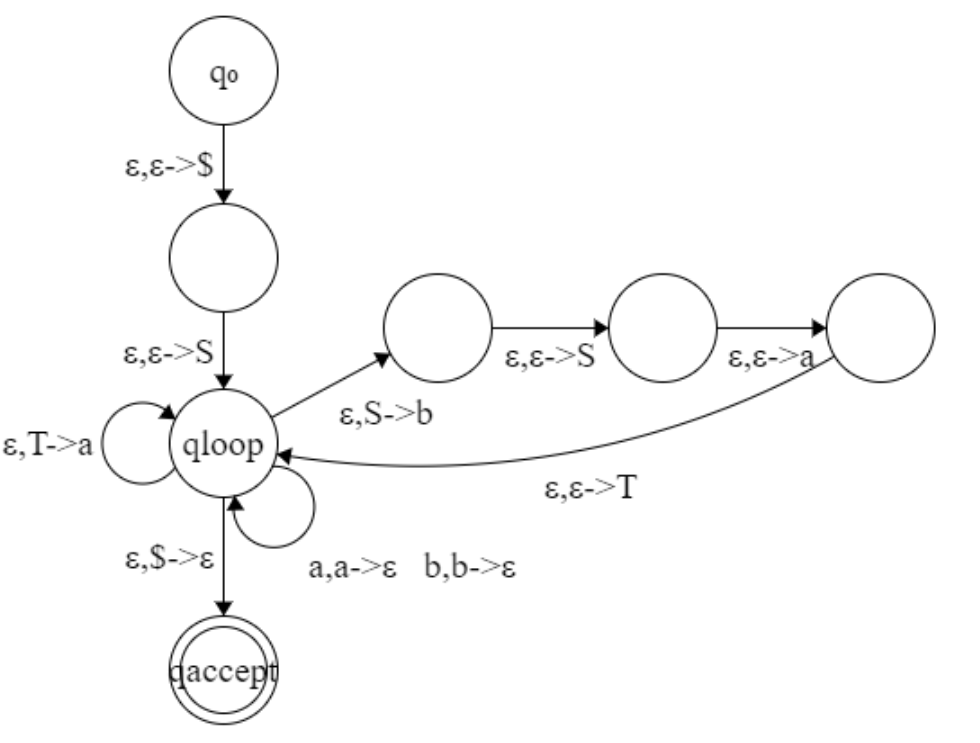
-
Add the compare of terminals:
![15]()
if the top of stack and the readin symbol is the same, then pop it.
Now we can transform any CFG to PDA. Another example:
![16]()
-
The other direction: transform PDA to CFG.
Given a PDA, for each pair of its states , we create a variable in the grammar. This variable will generates all the strings that can take the PDA from with an empty stack to with an empty stack. Obverve that such strings can also take the PDA from to with the same stack contents at and at .
Firstly, we need to modify the PDA slightly to give it the following three features:
- It has a single accept state, .
- It empties its stack before accepting.
- Each transition either pushes a symbol onto the stack, or pops one off the stack, but does not do both at the same time.
Then, we construct the grammar as follows:
-
For each , if we have the form:
then we add the rule: .
-
For each , add the rule A_{pq}\rightarrow A_{pr}A_
-
For each , add .
-
is the start variable.
You may get some insight for the construction from the following figures:
![18]()
Example:
![17]()
Theorem
Every regular language is context free.
Proof: obviously PDA can simulate any DFA.
Theorem
Context free language is closed under union.
Proof: Add the new rule .
Theorem
Context free language is closed under concatenation.
Proof: Add the new rule .
Theorem
Context free language is closed under star operation.
Theorem
Context free language is NOT closed under intersection.
Proof: is not context free.
Theorem
Context free language is NOT closed under complement.
Proof: We assume to the contrary, then . If CFL is closed under complement, then it should be closed under intersection, which is false.
Theorem
The intersection of a CFL and a regular language is context free.
Proof: For a PDA and NFA , we can construct a recognizing .
state: where .
transition:
if and only if in PDA and in NFA.
# Non-context-free languages
Theorem(Pumping lemma for context-free languages)
If is a context-free languages, then there is a number (pumping length) where, if is any string in of length at least , then may be divided into five pieces satisfying:
- for each ,
Proof: Say is the number of variables in , is the maximum number of symbols in the right side of a rule. We set to be .
If the parser tree’s height is , then the string it parses is at most long.
So if the length of string is greater than , then the height of the parser tree is bigger than , in other words, we definitely have two same variables in the longest path in the parser tree.
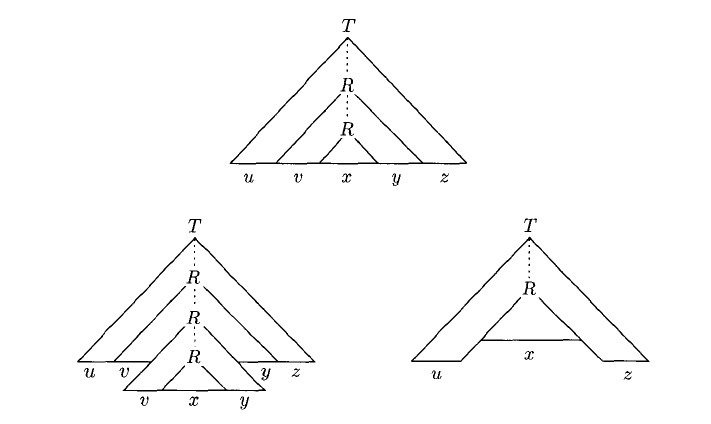
Then we can substitute the small substree by the bigger subtree (their roots are both) as the figure above, then condition 1 is satisfied since can always be parsed.
Condition 2 is natually satisified since we don’t have the derivation , so either or is not empty.
Condition 3 is a bit tricky. We need to modify to . Then the longest path in the parser tree is greater than still. We choose so that both occurences fall within tht bottom variables on the path. So the subtree is at most high (the bottom is terminals). Then we can guarantee that .
Example: is not context free, since for any , we can construct , it cannot be divided into five pieces satisfying three conditions.
# The church-turing thesis
# Turing machines
Definition(Turing machine)
A Turing machine is a 7-tuple, , where are all finite sets and
- is the set of states.
- is the input alphabet not containing the blank symbol .
- is the tape alphabet, where and .
- is the transition function.
- is the start state.
- is the accept state.
- is the reject state, where .
The configuration is
- a current state
- a string over the tape alphabet
- a string over the tape alphabet
the configuration means that, the current of turing machine is , the content of the tape is and the head location is at the first symbol of .
The configuration yields if:
-
-
or
Intuitively, it’s just modifying the head location content from to and move the head.
Remark(Important!): When the head is already at the leftmost location of the tape, then if we try to move it left, then it will stay still. Thanks to this property, we can easily move head to the leftmost.
If we enter the accept configuration (the state in the configuration is ) then the Turing machin will accept the input string. Similarly we have reject configuration. Both of them are called halting configuration.
Definition
Call a language Turing-recognizable if some Turing machine recoginizes it.
TM recognizes language means that for all string in , TM will accept it. While for strings not in , TM will reject or not halt.
Definition
Call a language Turing-decidable if some Turing machine decides it.
TM decides language means that for all string in , TM will accept it. While for strings not in , TM will reject it. The TM must halt.
Example: Here we describe a Turing machine that decides .
"On input string :
- Sweep left to right across the tape, crossing off every other 0.
- If in stage 1 the tape contained a single 0, accept.
- If in stage 1 the tape contained more than a single 0 and the number of 0s was odd, reject.
- Return the head to the left-hand end of the tape
- Goto state 1."
The stage 1 is cutting the number of 0s in half.
# Varaints of turing machine
A multiple Turing machine is like an ordinary Turing machine with several tapes. Each tape has its own head for reading and writing.
If we have tapes, then the transition functions is like:
means “stay”. So all tapes can do their own work or pause.
Theorem
Every multitape Turing machine has an equivalent single-tape Turing machine.
Proof: Say that has tapes, we can construct a single tape Turing machine to simulate its behavior.
= "On input :
-
First puts its tape into the format that represents all tapes of . The formatted tape contains:
-
To simulate a single move, scans its tape from the first @, which marks the left-hand end, to the st @, which marks the right-hand end, in order to determine the symbols under the virtual heads. Then makes a second pass to update the tapes according to the way that 's transition function dictates.
-
If at any point moves one of the virtual heads to the right onto a @, this action signifies that has moved th corresponding head onto the previously unread blank portion of that tape. So writes a blank symbol on this tape cell and shifts the tape contents, from this cell until the rightmost @, one unit to the right.
Then repeat the simulation."
Nondeterministic Turing machine can proceed different possibilities.
and it accepts the input string if any branch accepts it.
Theorem
Every nondeterministic Turing machine has an equivalent single-tape Turing machine.
Proof: We can use a three-tapes Turing machine to simulate nondeterministic Turing machine.
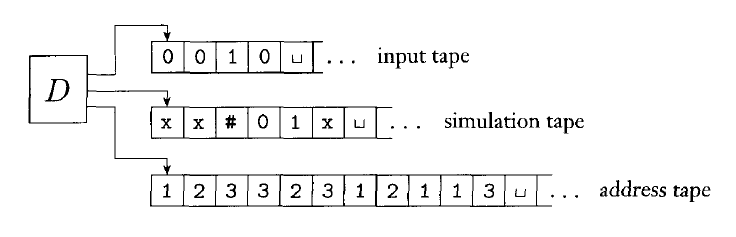
Let’s first consider the data representation on tatpe 3. Every node in the searching tree can have most children, where is the size of largest set of possible choices given by 's transition function.
To every node in the three we ssign an address that is a string over .
For example, we assign the address 231 to the node we arrive at by starting at the root, going to its 2nd child, going to that node’s 3rd child, and finally going to that node’s 1st child. Each symbol in the string tells us which choice to make next when simulating a step in one branche in 's nondeterministic computation.
If too few choices are available for a configuration, then the symbol is invalid.
Now we are ready to describe .
-
Initially tape 1 contains the input , and tapes 2 and 3 are empty.
-
Copy tape 1 to tape 2.
-
Use tape2 to simulate with input on one brach of its nondeterministic computation. Before each step of consult the next symbol on tape 3 to determine which choice to make.
If no more symbols remain on tape 3 or if this nondeterministic choice is invalid, abort this brach by going to stage 4. Also goto stage 4 if a rejecting configuration is encountered. If an accepting configuration is encountered, accept the input.
-
Replace the string on tape 3 the lexicographically next string. example:
Then repeat the simulation.
Theorem
A language is Turing-recognizable/decidable if and only if some nondeterministic Turing machine recognizes/decides it.
Definition(Enumerator)
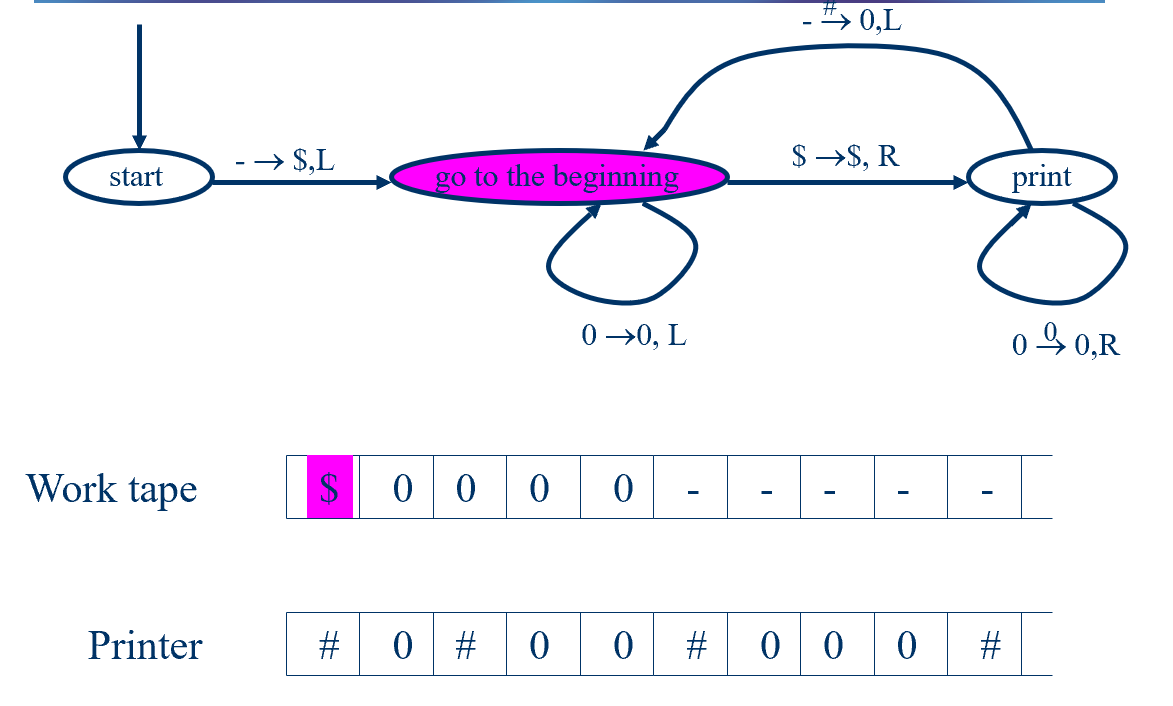
An enumerator is a TM with two tapes: the work tape and the printer.
-
Initially both tapes are empty.
-
On the work tape it can read, write and move just like the ordinary TM.
-
On the printer, it can only print one of the symbols of the language alphabet, or @ serving as the “end of string” symbol. So the transition looks like:
meaning “if in state , you see a symbol on the work tape, then replace it with , move in the direction , goto state and print to the printer”. Every time it prints a symbol, the head of the printer moves right. if is absent, then nothing happens to printer.
-
There is start state, but no accept or reject states. Entering a configuration from which there is no transition causes the enumerator to halt.
-
The language enumerated by an enumerator is the set of strings that it prints on the printer.
Example:
Theorem
A language is Turing-recognizable if and only if some enumerator enumerates it.
Proof: First we show that if we have an enumerator that enumerates a language , a TM recognizes it.
= "On input :
- Run . Every time that outputs a string, compare it with .
- If ever appears in the output of , accept."
Now we do the other direction
= "Ignore the input
- Repeat the following for
- Run for steps on each input
- If any computations accept, print out the correspoinding ."
where is a list of all possible strings in .
In fact, if accepts some string , then it will appear on the printer infinite times.
Church-Turing thesis: Intuitive notion of algorithms = algorithms defined by calculus = algorithms defined by Turing machines.
# Decidability
# Decidable languegs
Theorem
is a DFA that accepts input string is a decidable language.
Proof:
= "On input , where is a DFA and is a string:
- Simulate on input .
- If the simulation ends in an accept state, accept. If it ends in a nonaccepting state, reject."
Theorem
is a NFA that accepts input string is a decidable language.
Proof:
= "On input , where is a NFA and is a string:
- Convert to a DFA. Since the algorithm is precisely introduced before, it can be simulated by TM.
- Call decider."
Theorem
is a regular expression that generates input string is a decidable language.
Proof:
= "On input , where is a regular expression and is a string:
-
Convert to its corresponding NFA.
-
Call decider."
Theorem
is a DFA and is decidable.
Proof:
= "On input where is a DFA:
- Mark the start state of .
- Repeat until no new states get marked:
- Mark any state that has a transition coming into it from any state that is already marked.
- If no accept state is marked, accept; otherwise reject."
Theorem
and are DFAs and is decidable.
Proof:
= "On input , where and are DFAs:
-
Construct DFA , where
is called the symmetric difference of and .
-
Call to decider whether is empty, if is, then accept. Otherwise reject."
Theorem
is a CFG that generates string is decidable.
Proof:
= "On input where is a CFG and is a string:
- Convert to an equivalent grammar in Chomsky normal form.
- List all derivations with steps, where is the length of , except if , then check if we have the rule .
- If any of these derivations generate , accept; if not, reject."
Notice that if a string can be generated by a Chomsky normal form, then the number of derivation steps is at most .
Theorem
is a CFG and is decidable.
Proof:
= "On input where is a CFG:
- Mark all terminal symbols in .
- Repeat until no new variables get marked:
- Mark any variable where has a rule and each symbol has already been marked.
- If the start variable is not marked, accept; otherwise reject."
Theorem
are CFGs and is NOT decidable.
The proof is too hard now.
Theorem
Every context-free language is decidable.
Proof: Let be a CFG for context-free language , then on input string , we just need to call decider.
# The halting problem
Theorem
is a TM and accepts is undecidable.
Proof: We assume to the contrary that is decidable and has a decider :
Now we construct a new TM:
= "On input , where is a TM:
- Run on input .
- If accepts, then reject. If rejects, then accept."
Now what would happen if we run on input ?
Which is obviously a contradiction.
So doesn’t exists.
Theorem
A language is decidable if and only it’s Turing recognizable and co-Turing-recognizable (its complement is Turing recognizable).
Proof:
One direction: if is decidable, we can easily see that both and its complement are Turing-recognizable.
The other direction: if both and are Turing-recognizable, we let be the recognizer for and for . And we construct a Turing machine:
= "On input :
- Run both and on input in parallel (two tapes).
- If accept, accept; If accept, reject."
Theorem
is not Turing-recognizable.
Proof: We already know that is Turing-recognizable but not Turing-decidable. So its complement must NOT be Turing-recognizable.
# Reducibility
# Undecidable problems from language theory
Theorem
is a TM and halts on input is undecidable.
Proof: We assume to the contrary, if is decidable and is a decider. Then we can construct a decider for :
= "On input , an encoding of a TM and a string:
- Run on input .
- If rejects, reject
- If accepts, simulate on until it halts.
- If accepts, then accept; otherwise reject.
Since we already know that is undecidable, so does not exist. So is undecidable.
Theorem
is a TM and is undecidable.
Proof:
Like the last theorem, we can prove that, if we have the decider for , then will be decidable too.
We assume to the contrary, is a decider for .
We construct a decider for :
= "On input string where is a Turing machine and is a string:
-
Construct a new Turing machine :
= "On input string
- If , reject
- If , run on if accepts then accept."
-
Run on input .
-
If accepts, reject; otherwise accept."
Remark: We don’t need to run on , instead, we only need the encoding of doing such work.
Obviously, if and only if accepts .
Theorem
is a TM and is a regular language is undecidable.
Proof: We let be a decider that decides . Then we can construct a decider for :
= "On input , where is a TM and is a string:
-
Construct the following TM :
= "On input :
- If is of the form , accept.
- If does not have the form, run on input and accept if accepts ."
-
Run on input .
-
If accepts, accept; otherwise reject."
Remark: Firstly, we don’t need to run on , instead, we only need the encoding of doing such work.
Obviously, if accept , then . Because no matter of the input , will accept it. If doesn’t accept , then , since only , will accept it. So is regular accepts .
So if acceptes , then accepts .
Theorem
are TMs and is undecidable.
Proof:
If we have the decider for , then we can construct the decider for :
= "On input , where is TM
- Run on , where is the Turing machine rejecting any input.
- If R accepts, accept; otherwise reject."
Obviously, .
Theorem
is a CFG and is undecidable.
# Mapping reducibility
Definition
A function is a computable function if some Turing machine , on every input , halts with just on its tape.
Definition
Language is mapping reducible to language , written , if there is a computable function , where for every :
The function is called the reduction of to .
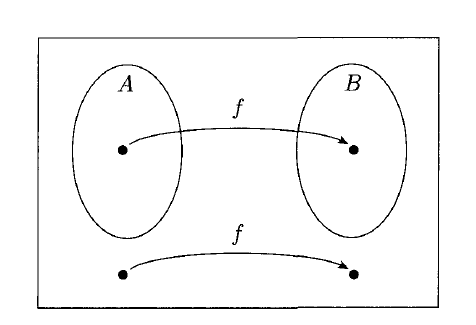
Theorem
If and is undecidable, then is undecidable.
Proof:
If we have a decider for , then for any input , we can compute and check whether it is in . Then we can decide whether is in .