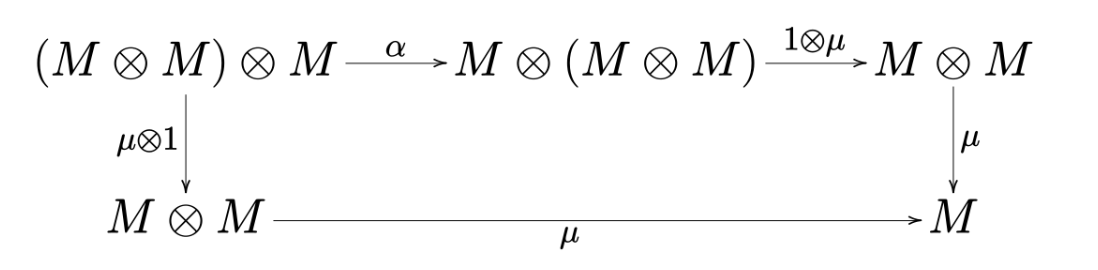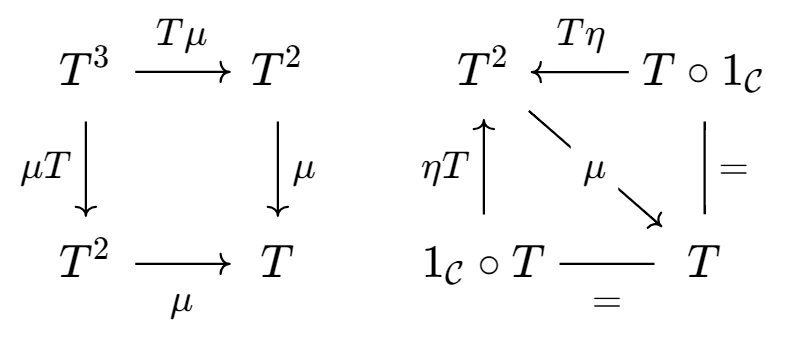我明明在努力工作,却隔三岔五都会遇到歧视这份职业的人。他们的眼神里,有着对反驳的胆怯与警戒,有时候,还藏着一种 “你敢反驳我便应战” 的好战光芒。
原本以为熟练在 Haskell 中用 Monad 和 Monad transformer 了,结果发现阅读文献碰到时还是绕不开数学。
# Monad 的前世今生
学习 Monad 的时候,如果我们想从数学角度理解,很容易就发现了这样的学习路程:
Haskell IO Monad->category theory->Kleisli category->Kleisli triple->algebraic theory
所以我们直接从 algebraic theory 开始,从最抽象的一步步具化到 Monad。
我们基于集合论先进行讨论,然后再用范畴论的语言重述。
# 集合论语言
首先,我们定义一个极其抽象的,称之为 “operator domain” 的东西(用Ω 表示)。它是一个集合序列Ω≜(Ω1,Ω2,Ω3,...)。
它可以说是毫无信息量了,只表达一个信息:对于ω∈Ωn,我们将ω 看作一个由n 指向 1 的箭头。
Example:
譬如Ω=({e},{i},{m},∅,∅,...),可以用下图表示:
![6]()
然后我们引入Ω-algebra 的概念。一个Ω-algebra 是一个 pair (X,δ),其中X 是一个集合,而δ 是一系列函数,对于ω∈Ωn,有函数δω:Xn→X。
Example:
延续上面的Ω 定义,我们可以考虑这样一个Ω-algebra:
X={0,1}δe:⊥↦1δi:0↦0,1↦1δm:(0,0)↦0,(0,1)↦1,(1,0)↦1,(1,1)↦0
可以看出来,(X,δ) 其实把Ω 中的e "翻译" 成了单位元,i 翻译成了逆元,m 翻译成了模 2 加法。
对一个集合A,实际上我们可以定义AΩ 是一个集合,里面的元素被称为 "terms",是由A+Ω 中的 symbol 组成的 “合法字符串”。
这个说法很抽象,不妨看一个例子
Example:
延续上面Ω 定义,我们可以考虑A={x,y,z} 时,那么下面的字符串都是AΩ terms:
x,xym,e,xi,xymzm,xyim∈AΩ
实际上,“合法” 体现在可以被当作后缀表达式 parse 掉。譬如xym 因为m∈Ω2,可以把它看作一个二元运算符,前面就需要加两个合法的AΩ 中的 terms。而xi 因为i∈Ω1 所以前面只需要加一个 term 就好。
可以注意到,严格来说我们是A+Ω,但实际中我们几乎默认A 和Ω 没有公共元素(A 看作 elements,Ω 看作 operations)所以往往直接写x,y,m 而不是(x,0),(y,0),(m,1)。
我们继续可以引入Ω-equations 的概念。它也是一个集合,而集合中的元素全部是二元集合。
我们给定一个毫无意义,但是方便 enumerate 的集合V={v1,v2,v3,...} 表示抽象的 variable,那么看一个例子:
Example:
延续上面Ω 的定义,我们可以定义Ω-equations:
E={{v1v2mv3m,v1v2v3mm},{v1v1im,e},{v1iv1m,e}}
虽然看起来很奇怪,但是仔细理解,可以发现它表达了(v1+v2)+v3=v1+(v2+v3),还有v1+(−v1)=0 这种含义。
然而这个E 之所以使用的是二元集合而不是等号,是因为VΩ 中的 terms 是无法判等的!只能等它被某个Ω-algebra 解释后,才可以去判等。
定义好Ω 和E 后(对于某个V),那么(Ω,E) 就被称为一个 equational presentation。
因为实际上,它只定义了一些 operations 的 domain,还有一些 equational relation。剩下我们一无所知。这个 operation 是什么?加法?这个 equational 是什么?同构?相等?v1,v2 是什么?整数?我们都不知道!这就是抽象。
然而有了Ω-algebra,这就都不一样了!我们知道了元素是X 中的,我们知道了应该怎样运算(利用δ)。
Example:
给定Ω-algebra (X,δ) 后,很显然我们得到了一被称为 total description map 的东西:δ∗:XΩ→X,递归定义为:
xδ∗=xp1p2...pnωδ∗=p1δ∗p2δ∗...pnδ∗δω
仔细看看就知道它这是在利用δ 在进行计算!计算结果就还是X 中的元素。
那么,给定一个r:V→X 把抽象的 variable 映射到具体的X 中的元素,很显然我们可以诱导出r†:VΩ→XΩ→X。即我们先把VΩ 中 terms 里的 abstract variable 换成X 中的元素,再利用δ∗ 进行计算。
此时我们可以引出(Ω,E)-algebra 的定义了!(注意,之前的 algebra 是没有E 的)
(Ω,E)-algebra 是一个Ω-algebra (X,δ),并且X 中的元素是可以判等的。
对于任意的 assignment r:V→X,都有E 中的 equation 条件被满足(相等)。
注意,这里说了对于任意 assignment,实际上也就是x+(−x)=0 for all x 的意思。而这里的 for all 体现在把 abstract variable 映射到具体元素函数r 的任意上。
能用Ω,E,δ,X 这样定义出的(Ω,E)-algebra 被称为 equationally definable class of algebra。
于是对于任意 set A,如果我们有 function f:A→X,那就可以自然地 extend 出一个f†:AΩ→X 的出来。
之前说了,VΩ 中的 terms 是无法判等的,那么现在给定一个 equational presentation (Ω,E),和一个任意的集合A,我们定义一个AΩ 上的等价关系:
EA={(p,q)∈AΩ×AΩ∣for all (Ω,E) algebra (X,δ) and functions f:A→X,f#p=f#q}
Example:
沿用之前的定义:
Ω=({e},{i},{m},∅,...)E={{xymzm,xyzmm},{xxim,e},{xixm,e},{exm,x},{xem,x}}
那么很显然,对于A={x,y,z} 有:
p=xxximm∈AΩq=x∈AΩ
而p=q。这是一件很自然的事,因为要满足E,就自然会导致p,q 在所有(Ω,E)-algebra 下是相等的。
EA 的定义,就是把原先AΩ 这个不可比的集合,利用E 而引入了等价关系变得可比!
我们记AT=AΩ/EA(T is for ‘‘theory’’),并且自然地引入一个映射Aρ:AΩ→AT,也就是把p∈AΩ↦[p]∈AT。
Example:
沿用上述的定义,实际上我们有:
[xxximm]=[xem]=[x]
它们都是一个等价类里的(可以看作是化简)
实际上,AT 就是一个(Ω,E)-algebra!这是怎么定义的呢?
X≜AT=AΩ/EA[p1][p2]...[pn]δω≜[p1p2...pnω]δω:ATn→AT
那么给定一个 equational presentation (Ω,E),我们可以定义:
The clone of (Ω,E) is a category named Set(Ω,E):
- 它的 objects 是 sets A,B,C,...。
- 它的 morphism A⇁B 是 function A→BT。
- 它的 identity morphism 是Aη:A→AT。
- 它的 composition 定义为(AαB)∘(BβC)=AαBTβ†CT。
Example:
考虑Ω=({e},{i},{+},∅,∅,...),以及E=∅。那么此时显然EA=∅ 对于任意A,所以也有AT=AΩ/EA=AΩ。
假如我们有四个集合:
A={1}B={b,x}C={c,y}D={d,z}
然后有三个函数:
α:A→BT=BΩβ:B→CT=CΩγ:C→DT=DΩ
函数内容为:
α=β=γ=1↦xie+b+x↦yb↦cc+c↦dz+iy↦e
那么有:
α∘(β∘γ):A→DT(α∘β)∘γ:A→DT
且:
(β∘γ)=α∘(β∘γ)=(α∘β)=(α∘β)∘γ=b↦dz+idz+i+x↦e1↦eie+dz+idz+i++1↦yie+cc++1↦eie+dz+idz+i++
所以有α∘(β∘γ)=(α∘β)∘γ。
上个例子其实说明了,morphism 就是 substitution 的过程,也其实揭示了证明的内涵:证明某个命题,本质上就是一直在 substitute axiom 中的 variable。
到这里或许读者已经初见端倪,为什么我们应该把 Monad 理解成一种 computation。
因为从只含有 variable 的集合A,后面引入了Ω 中定义的 operations 得到AΩ,然后进一步引入了E 中的相等关系得到了AT。
AΩ 中的 terms 可以看作是表达式了,而AT 中的元素则可以看作有了E 给的化简规则后,化简的结果。
而 terms in AΩ 就可以看作是证明(Curry-Howard 同构),morphism A→BT 就告诉我们,得到了一个AT 中的 terms,如何通过 substitution 得到一个BT 中的 term。
这时候,我们会发现没有 types 怎么办。所以我们需要引入 2-category!!
object 是 types,morphism 是 terms,然后 morphism 之间的 morphism 是 substitution。
以下为原始 note:
# 单位半群(Monoid)
” 这个相对简单,就是一个代数结构。当集合S 上存在一个二元运算∗:S×S→S 和一个单位元e∈S 满足:
-
∀a∈S,e∗a=a∗e=a.
-
∀a,b,c∈S,a∗(b∗c)=(a∗b)∗c.
那我们就称集合S 和这个运算、单位元形成了一个单位半群(幺半群,Monoid)
例:自态射形成了一个 Monoid。考虑一个 category C 中只有一个元素a 和很多 morphism,那么这些 morphism 都是从a 到a 的箭头,他们形成了一个 Monoid。其中S 就是这些 morphism,二元运算是 morphism 的组合,单位元是 identity morphism。由于 category 的性质,故满足结合律和单位律,故形成了一个 Monoid。
# Monoidal Category
A monoidal category is a category C quipped with a monoidal structure:
-
a bifunctor ⊗:C×C→C.
-
an object I called the monoid unit.
-
three natural isomorphisms:
-
for any three arguments A,B,C, there is a isomorphism α:
αA,B,C:A⊗(B⊗C)≅(A⊗B)⊗C
-
for any argument A, there are two isomorphisms:
λA:I⊗A≅AρA:A⊗I≅A
-
the three natural isomorphisms should satisfy the coherence conditions:
-
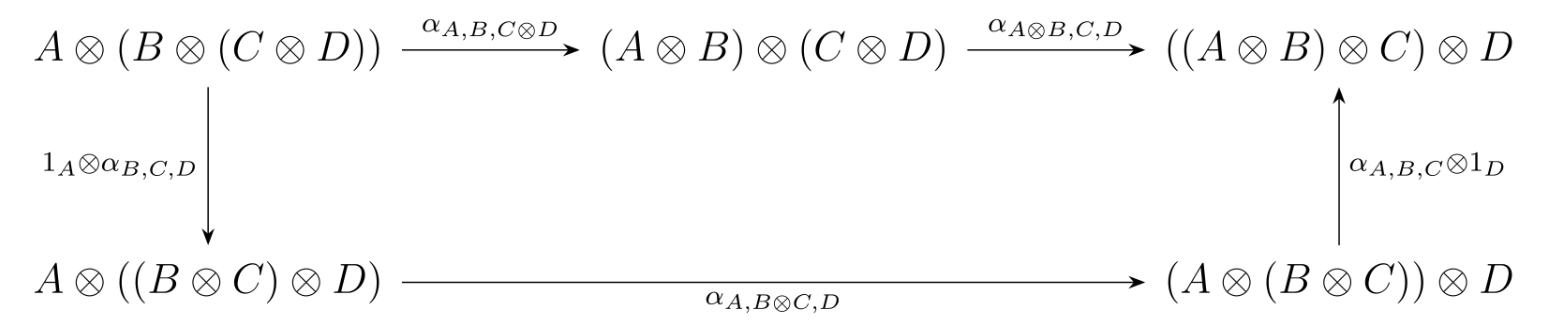
for all A,B,C,D∈C, the following diagram commutes:
![1]()
-
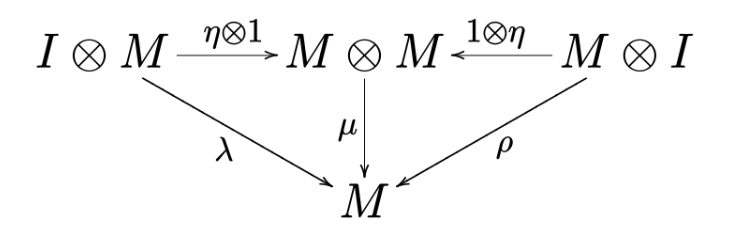
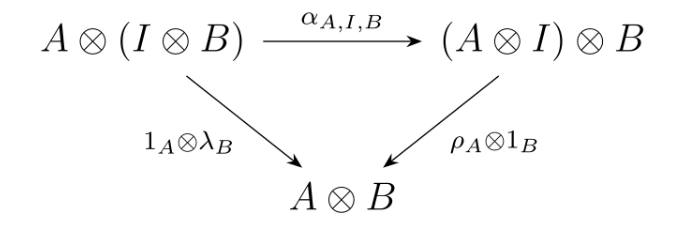
for all A,B∈C, the following diagram commutes:
![2]()
关于这个定义,可以说明几点。
-
这个 monoidal structure 里的元素(譬如单位元),都是 category C 里面的 object。也就是说我们希望这个 category 本身就有一点 monoid 的结构。但是它不是一个 monoid 在于,结合律和单位律都是同构而不是相等。譬如在 category Set 中,就是集合的同构而不是集合的相等。{(a,(b,c))} 和{((a,b),c)} 就是同构但不相等的。
-
其次下面的 coherence conditions 其实是,我们可以利用α 找出很多个诸如下面这种同构:
(((A1⊗A2)⊗A3)⊗...⊗An)≅(A1⊗(A1⊗(A3⊗...⊗An)))
因为你可以选择拆括号时不同的顺序,从而选择α 的不同的 arguments。coherence condition 就说明,这些同构都应该是同一个。
例:把 category Set 补充成一个 monoidal category。bifunctor 选择笛卡尔积,即A⊗B={(a,b)∣a∈A,b∈B}。然后 unit object 选择为一个特殊的单元素集{∗}。可以验证譬如{((1,2),3),((4,5),6)}≅{(1,(2,3)),(4,(5,6))},以及{(1,∗),(2,∗)}≅{1,2} 这样有自然的 isomorphism 满足要求和 coherence condition。
# Monoid in monoidal category
下面我们定义,在一个 monoidal category 上自然导出一个 monoid:
A monoid (M,μ,η) in a monoidal category (C,⊗,I) is an object M together with two morphism μ,η:
- μ:M⊗M→M called multiplication.
- η:I→M called unit.
such that the diagram commutes:
![3]()
![4]()
例:考虑Set 是一个 monoidal category,那么我们选择其中一个 object,譬如M={0,1}。那么M⊗M={(0,0),(0,1),(1,0),(1,1)}。我们可以找到一个 morphism μ,即模 2 乘法:
μ(0,0)=0μ(0,1)=0μ(1,0)=0μ(1,1)=1
对于η,我们需要找到一个{∗}→{0,1} 的映射,很显然有两个选择。如果我们选择η∗=0 会怎样?那么第二个 diagram 将不 commute!因为I⊗M⟶η⊗1M⊗M⟶μM 就会有映射:(∗,1)↦(0,1)↦0,显然这和直接用消去映射λ(∗,1)=1 得到的结果不一样。
所以我们需要选择η∗=1,这样就满足了要求。这个例子也阐释了,我们是怎么利用已有的 monoidal category 中那些 monoid structure(即α,λ,ρ)构造一个 monoid 的。
# Monad
最终我们定义一个特殊情况:Monad is a monoid in the (monoidal) category of endofunctors.
考虑一个 category C,显然可以找到一个 category D:
- D 中的 object 是C→C 的 functor。
- D 中的 morphism 是 functor 之间的 natural transformation。
那么D 是一个 monoidal category:
- 对于两个 functor F,G∈D,F⊗G=F∘G∈D。
- I=1C 即C 上的 identity functor。
不难验证,这满足 monoidal category 的要求。实际上,D 是一个 strict monoidal category,因为根据 category 和 functor 的要求,实际上就有F∘(G∘H)=(F∘G)∘H,即不是同构而是直接相等。
那么我们就可以找出D 中的一个元素和两个 morphism,然后导出一个 monoid,即是 monad:
A Monad on C consists of an endofunctor T:C→C together with two natural transformations η:1C→T and μ:T∘T→T.
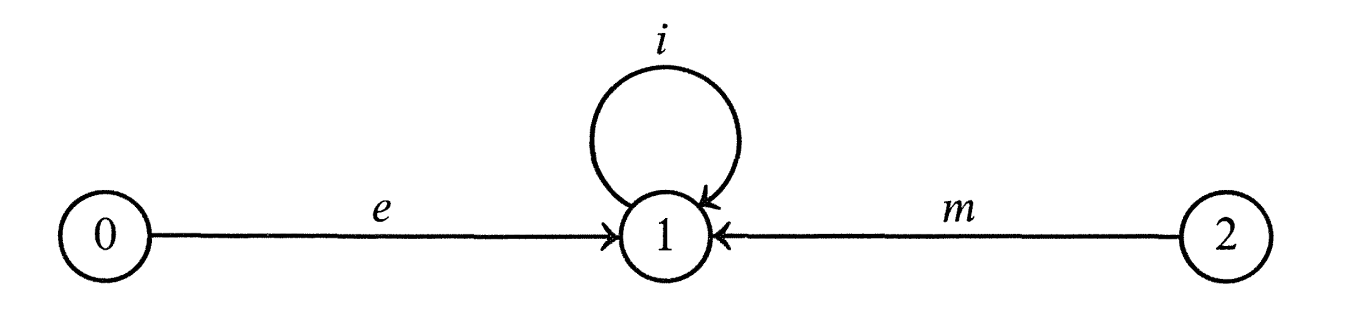
They are required to make the following diagram commutative:
![5]()
显然T 是D 中的一个元素,而μ,η 也对应了导出 monoid 在 endofunctor category 下的情况。而特别的地方在于,由于 endofunctor category 是 strict monoidal category,那么α,λ,ρ 都是单位映射,即相等(因为在 category 里,要求了1C∘T=T∘1C=T)。所以图中省略了α 部分,把T∘(T∘T) 和(T∘T)∘T 直接合并了,而且在右图中将λ,ρ 改写为=。
例:我们仍考虑 category Set,那么 powerset 实际上就是一个 Monad。考虑一个 endofunctor T(A∈Set)=2A∈Set,那么我们可以定义ηA:1Set(A)→T(A) 为ηA(a∈A)={a},譬如对于A={1,2,3},那么A↦ηA{{1},{2},{3}}。
然后定义μA:T(T(A))→T(A) 其实就是把集合 flatten 一层。譬如对于A={{{1,2},{3,4}},{{5}}},那么A↦ηA{{1,2,3,4},{5}}。这就形成了一个 Monad。
注意,实际上 functor T 应该不仅描述了 object 间的映射关系,还需要说明 morphism 间的映射关系。而Set 上的 morphism 是集合之间的函数,那么对于 powerset 这个T,一个很自然的映射就是把函数(譬如f(x)=x+1)apply 在 powerset 里的每个 set。
![1]()
![2]()