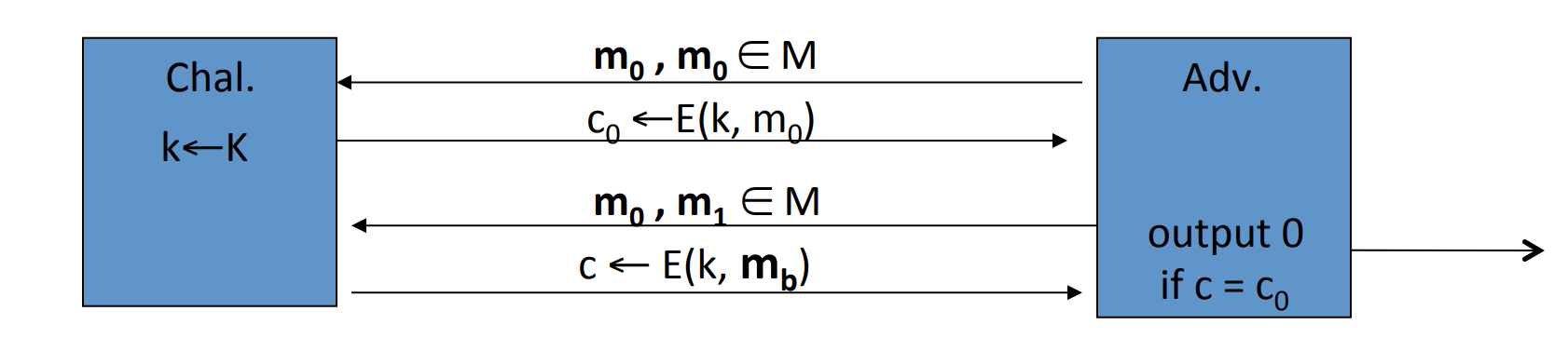就在这瞬间,黎明的晨星躲到云中了。
# Stream Ciphers
# What is a Cipher?
Definition: A cipher defined over is a pair of “efficient” algorithms where:
where is referred as key space, is referred as message space, is referred as cipher space.
Sometimes we also use notation PT (Plain Text) and CT (Cipher Text).
The function is called encryption and is called decryption. While means the consistency that given a key , then for any message , the decryption of the encryption of is .
What is also important that we always assume that the function and are open to the public, while only the key is kept secret.
- Example:The One Time Pad
OTP(Vernam 1917)
Where is bitwise xor. The One Time Pad is fast and secure if we choose the randomly. However, it needs as long keys as the plain text.
# What is a secure cipher?
Let’s assume that the attacker only have the CT , and the secruity requirement is that the attacker cannot get any information from it.
Definition (Information Theoretic Security, Shannon 1949): A cipher over is perfect secrecy if:
where means that subjects to the uniform distribution over .
The definition indicates that given CT can’t tell if the message is or , in other words, the attacker cannot get any information about PT from the CT .
However, other attacks (not only from CT ) may be possible.
Lemma: OTP is a perfect secrecy cipher, it reveals nothing about PT .(except possible maximum length, from wikipedia).
Proof: First given a message, we can pad it with 0 to the maximum length of . Then:
because , so the number of keys satisfying this condition is .
Then the proof is self-evident, since for any PT and CT , the probability of encryption is all the same.
Theorem: If a cipher over is perfect secrecy, then:
Which indicates that if we want a cipher to be perfect secrecy, we need to have at least as many keys as messages, which is impractical.
# Pseudorandom Generators
How to make OTP more practical?
- Idea: to replace the “random” key by “pseudorandom” key, which is much smaller.
Definition: A pseudorandom generator PRG is a “efficient” function:
where is called the seed space.
Then .
Now since the length of is much smaller than plain text, so it’s impossible to be perfect secure. However, we will define other security requirements later.
Definition: A PRG is predictable if there exists an “efficient” algorithm such that:
where is a non-negligible const.
The definition says that, the PRG is predictable if there exists an algorithm, which is able to predict the bit of the output given the first bits of the output. And works well in most cases.
- Example: random() function if glibc:
is a typical weak PRG and should NOT be used for crypto.
# Negligible vs. Non-negligible
- In practice: Whether is negligible is defined as a scalar, e.g. is non-negligible since it is likely to happen in 1GB data.
- In theory: is a function . is negligible if congruent to 0 faster than . While is non-negligible otherwise.
# Attacks to OTP
# Two time pad is insecure!
If we use the cipher key more than once:
then the attacker can get by xoring .
There are enough redundancy in English and ASCII to recover by knowing .
- Real world examples:Project Venona, MS-PPTP
# OTP is malleable and provides no integrity!
which means that tha attacker can easily modify the plain text even don’t need to know about it.
If the attacker get a CT , then he can modify it by , and send it back. The receiver will decrypt it as , which is modified by the attacker.
# What is a secure PRG ?
Definition: A statistical test on is an “efficient” algorithm , s.t. outputs “0” or “1”.
- Example: outputs “1” iff . Meaning that if the number of 0 and 1 is not too different, then the test believes that the string is random.
Definition(Advantage):let be a PRG and a statistical test on , then the advantage is defined as:
which says given a stat. test , whether can tell the difference between PRG and a real random.
Definition: We say a PRG is a secure PRG if “efficient” statistical test , is negligible.
Lemma: a predictable PRG is insecure.
Proof: if is a predictable PRG , then there exists a predict algorithm satisfying:
Now we can define a statistical test separating and random:
For real random, we have:
because in real random, and are of the same probability.
and we have:
then:
QED.
Theorem(Yao’82): an unpredictable PRG is secure.
Definition: Let be two distributions over , then we say are computationally indistinguishable if for any “efficient” statistical test ,
is negligible. Denoted as
# Semantic security
Definition: We say a cipher over is semantically secure if:
where is a probability distribution over .
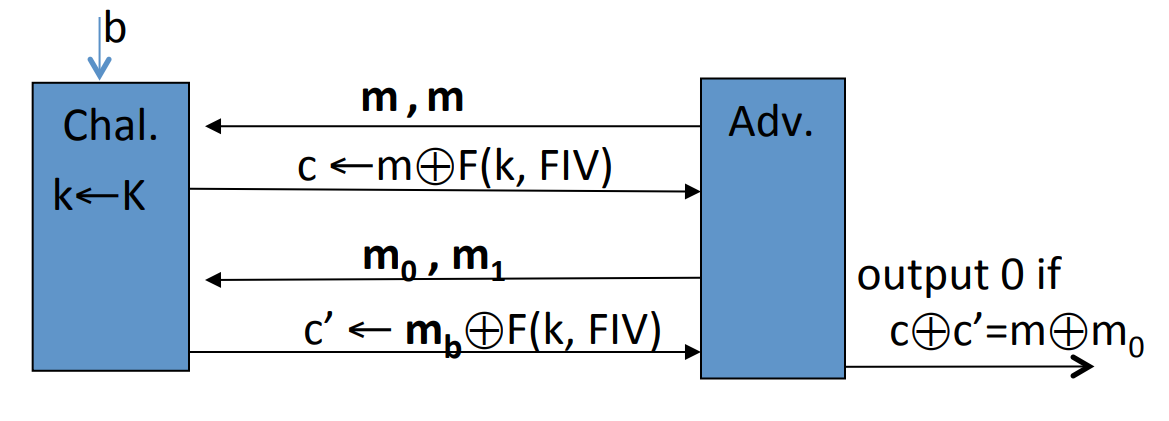
Given and an “efficient” algorithm , we can define two experiments:
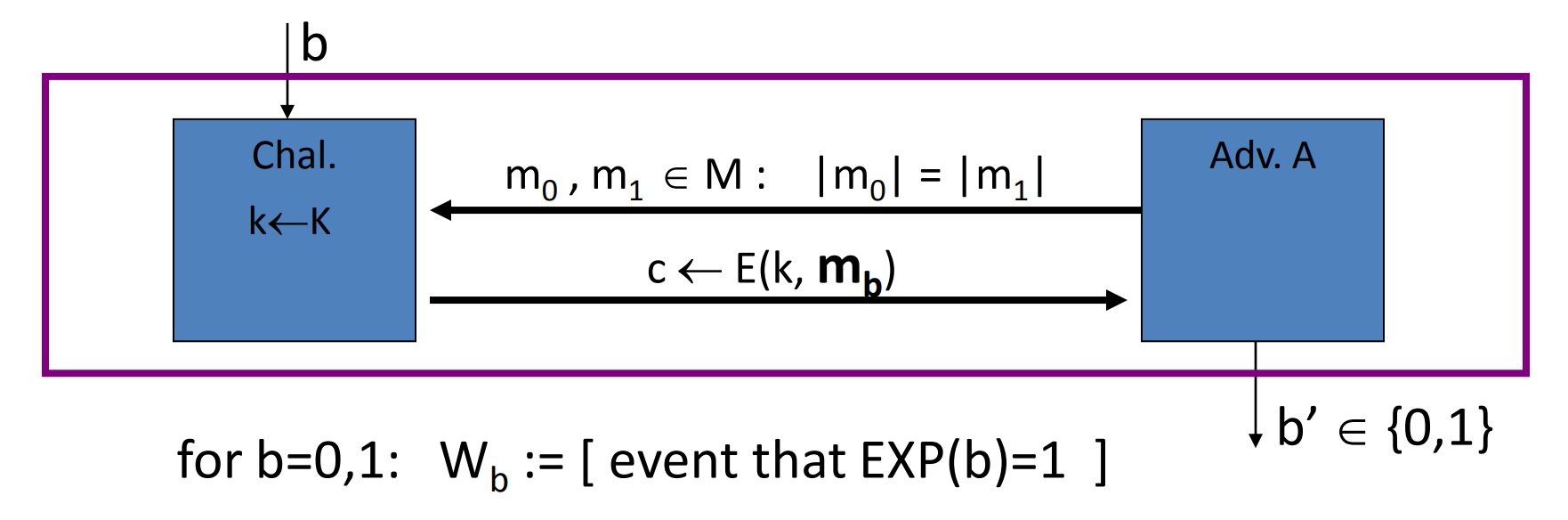
Adversary give two messages to the challenger, then the challenger will give back the cipher text determined by and randomly chosen . But don’t know , then will guess the value of .
Let is "when and is randomly chosen, the probability that guess ".
And let is "when and is randomly chosen, the probability that guess ".
Let’s define:
then is semantically secure if for any , is negligible.
- Example: Given a cipher, which we can guess the last bit of
PTbyCT. Then we can construct a :- choose two messages with different last bit.
- pass to the challenger.
- after receive the
CT, guess the last bit ofPTbyCT. - output the guess.
in this case, . Since can always guess right. So it’s not semantically secure.
Lemma: Perfect secure Semantically secure.
Proof:obviously,
# Stream ciphers are semantically secure
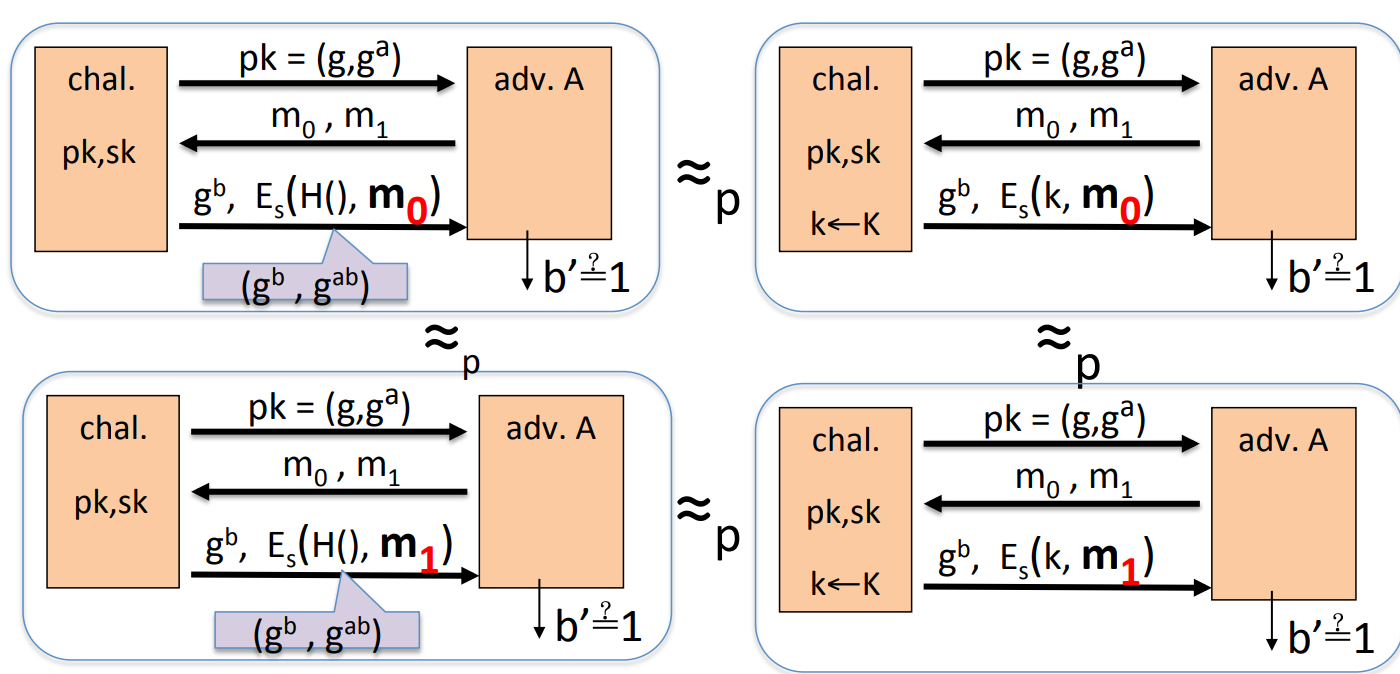
Theorem: Let be a PRG , then is a secure PRT stream cipher OTP derived from is semantically secure.
Proof: we just need to prove that, adversary , s.t.
Given an adversary , we can construct two experiments:
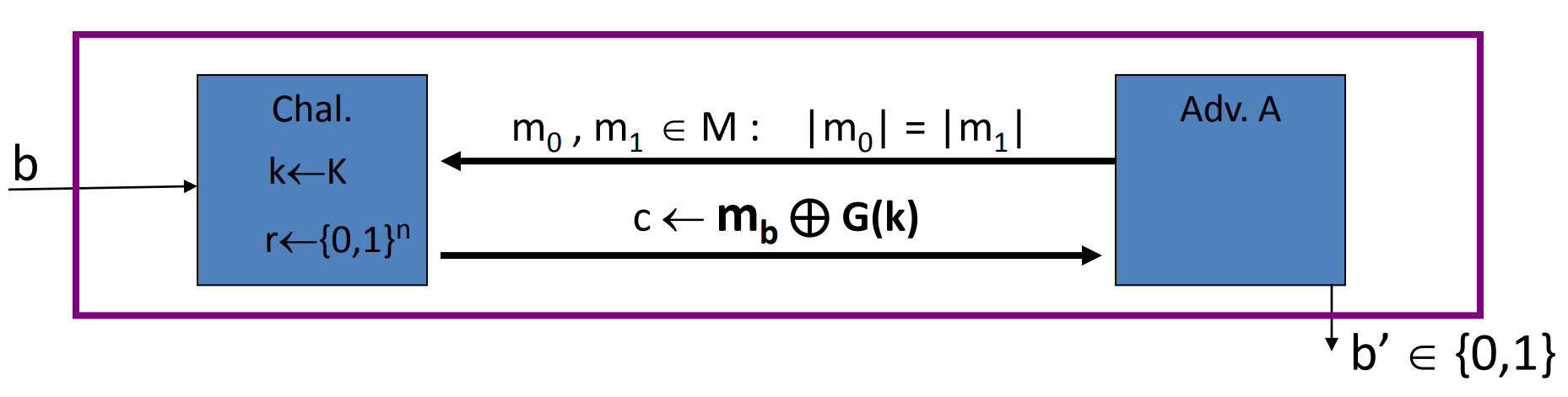
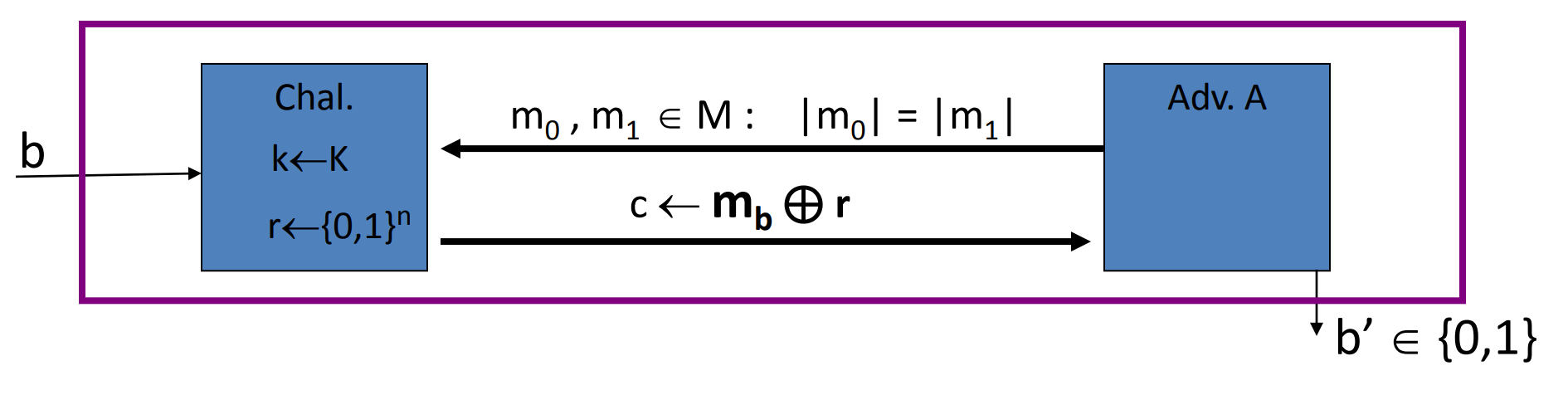
one using and one using real random to crypt.
Let is when , the guess of first exp is 1.
Let is when , the guess of first exp is 1.
Let is when , the guess of second exp is 1.
Let is when , the guess of second exp is 1.
Since OTP is perfect secrecy when real random:
Next we need to construct an adversary to PRG , and prove:
We can construct as follows:
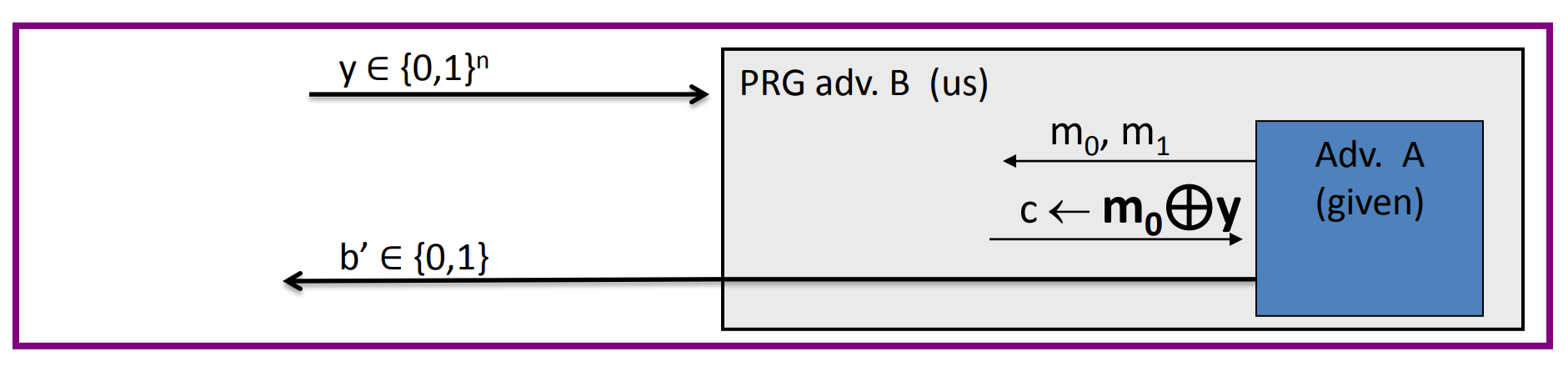
then
then:
So:
Since , so:
So if PRG is secure, then is negligible, then is negligible.
QED.
# Block cipher
# What is a block cipher?
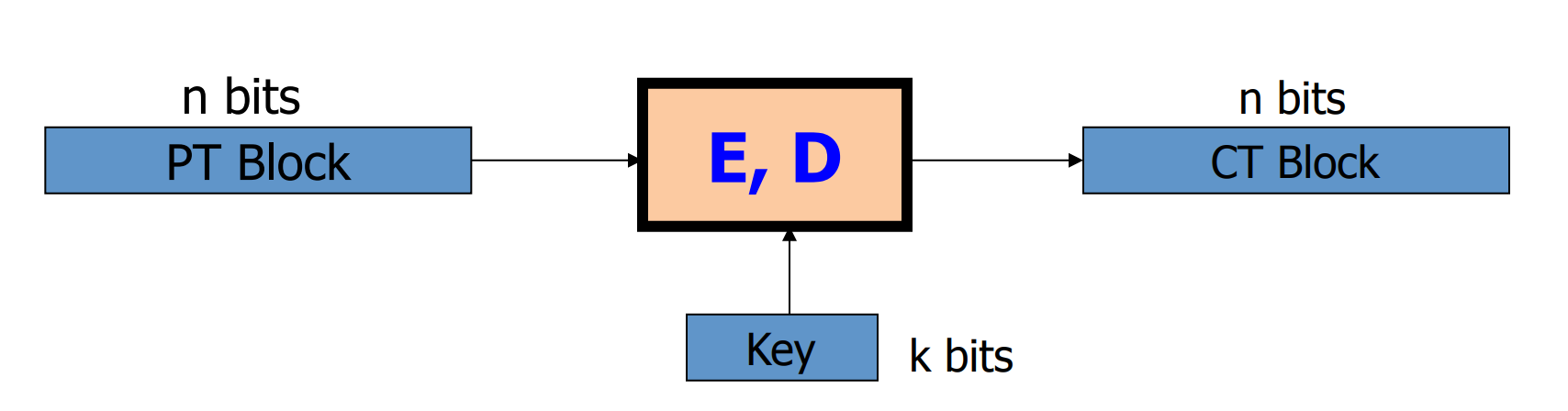
- Example: 3DES,n=64,k=168
- Example: AES,n=128,k=128 or 192 or 256
The process of encryption is:
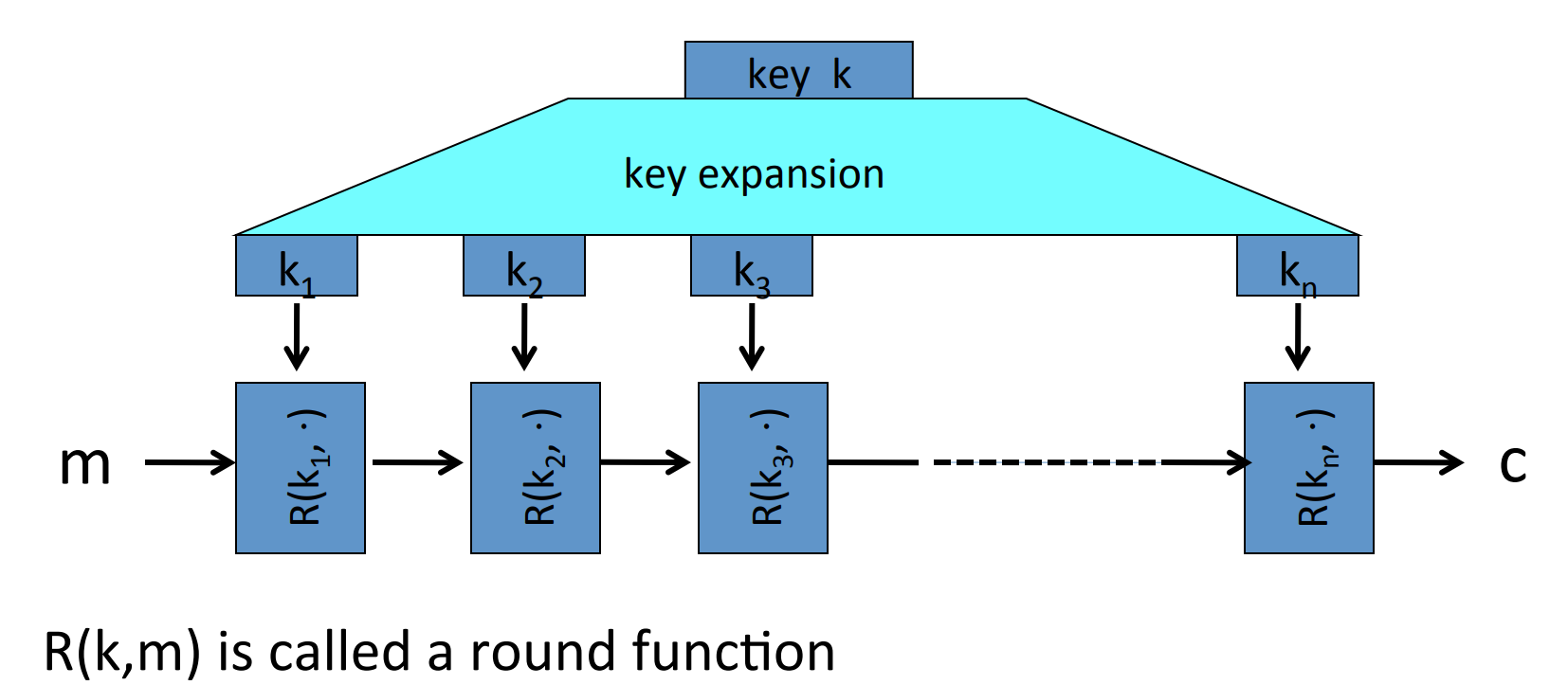
for 3DES,n=48; for AES,n=10.
Definition: Pseudo Random Function PRF defined over :
such that exists an “efficient” algorithm to evaluate .
Pseudo Random Permutation PRP defined over :
such that :
- Exists “efficient” deterministic algorithm to evaluate .
- The function is one-to-one.
- Exists “efficient” inversion algorithm .
- Example: 3DES, where .
Definition: Let be a PRF and . Then the PRF is secure if a random function in is indistinguishable from a random function in .
- An easy application: let be a secure
PRF, then we can construct a securePRG:
the PRG is parallelizable and is secure.
# Data encryption standard (DES)
The core idea of DES is Feistel Network: Given functions , build an invertible function :
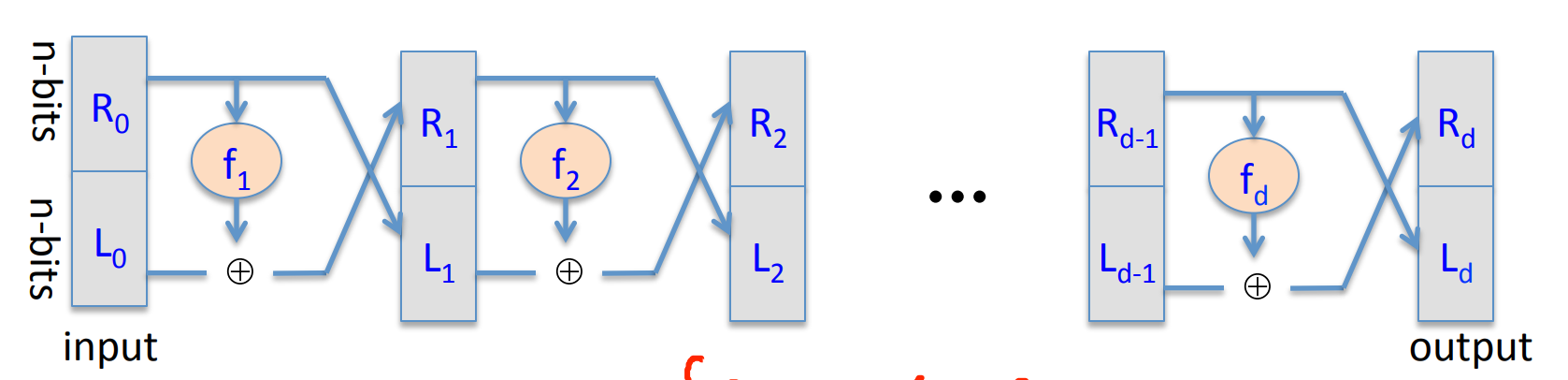
where
It’s easy to construct the inverse network:

where
Theorem(Luby-Rackoff’85): if is a secure PRF , then 3-round Feistel Network is a secure PRP .
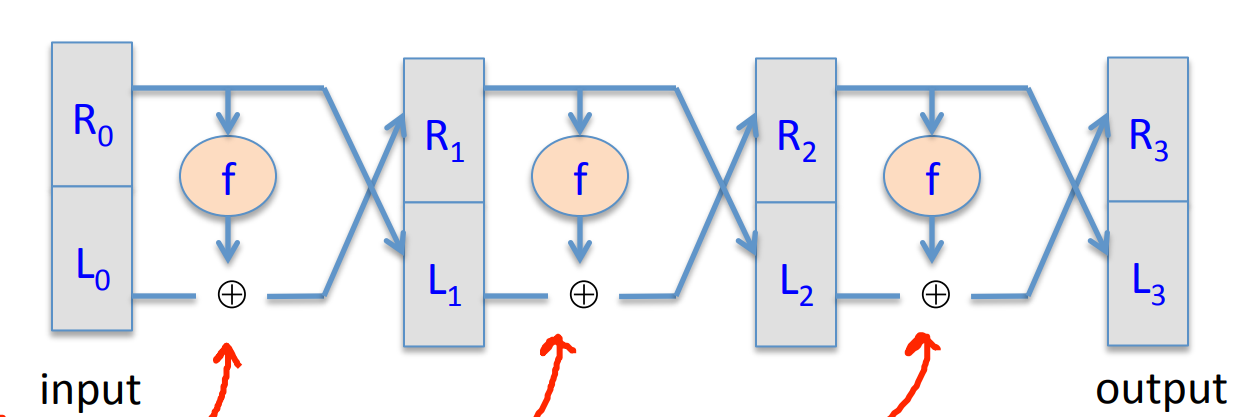
The DES is a 16-round Feistel Network, the Key size is 56 bits and block size is 64 bits, in other word, :
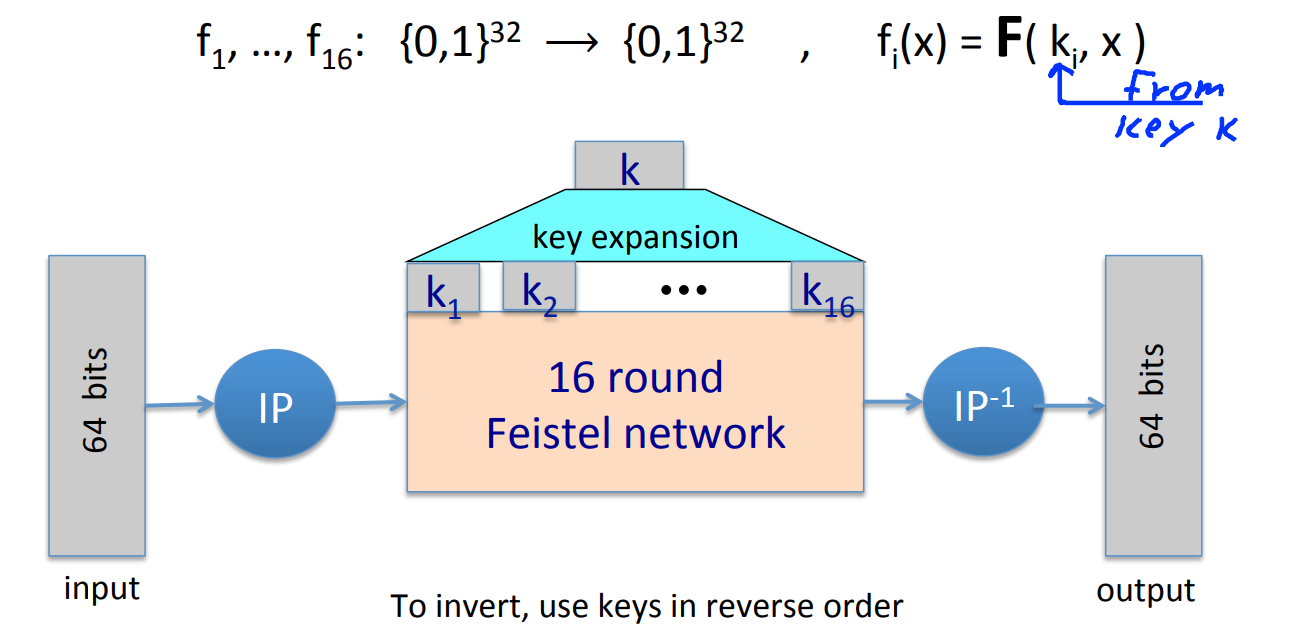
where works as follows:
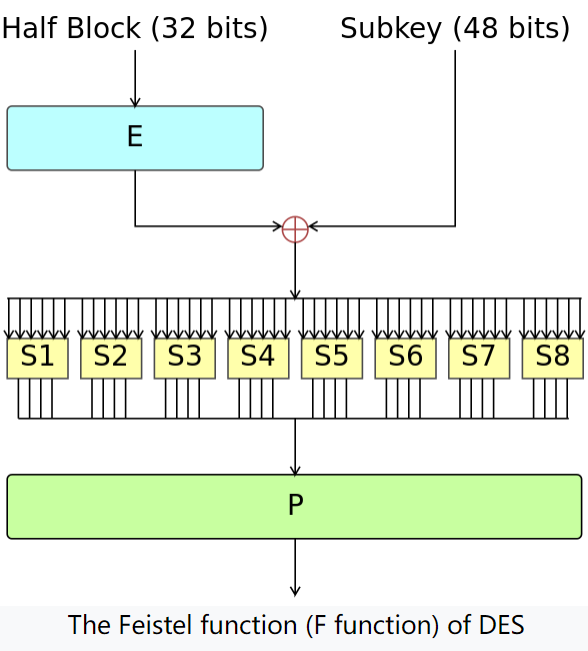
where half block is and subkey is . “E” stands for some shifts and expand tricks, “P” is for permutation, while the “S” S-Box are functions . The choice of S-Box function matters a lot.
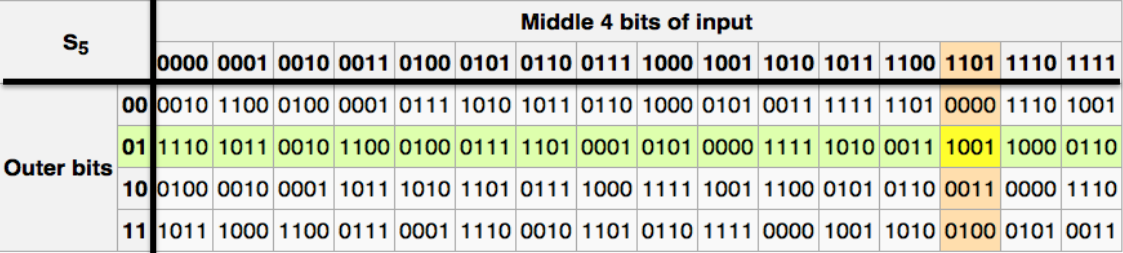
If the S-Box is linear, like:
then we can rewrite it in matrix as .
Then the DES is entirely linear, and we have:
which is insecure.
Choosing S-Box and P-Box randomly would result in an insecure block cipher, the key would recover after outputs [BS’89]
There are several rules to choose P-Box and S-Box, the most important one is never choose any linear function.
# Exhaustive Search for block cipher key
Goal: given a few input output pairs , find the key .
Lemma: Suppose DES is an ideal cipher (indistinguishable from a random permutation function ), then , there is at most one such that with probability .
Proof:
so the probability that there does not exists is .
QED.
For two DES pairs , the prob. that key is unique is .
So with exhaustive searching method, we can find the key in time .
We can strengthen DES against exhaustive search.
Method 1: Triple-DES, let as
for 3DES, key size=168 bits.
Why we don’t use Double DES ? like ?
We will introduce a Meet in the middle attack:
since
Then we can construct a table:
and sort the table by the second column .
Then we can enumerate , and binary search in the table, to find .
So the total time is which is not large enough.
Method 2: DESX
Define
It’s noteworthy that if DESX is defined as or , then it does nothing, it’s as vunerable to exhaustive search as DES.
# AES block cipher
Advanced Encryption Standard AES
Key size: 128 or 192 or 256 bits
Block size: 128 bits
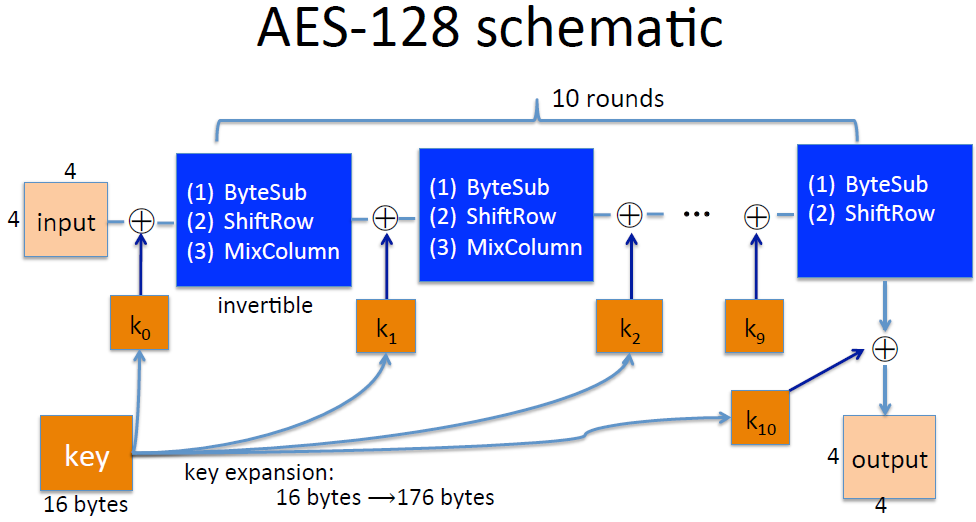
where the input is 4x4=16 bytes and the key is 16 bytes.
each round contains 3 function:
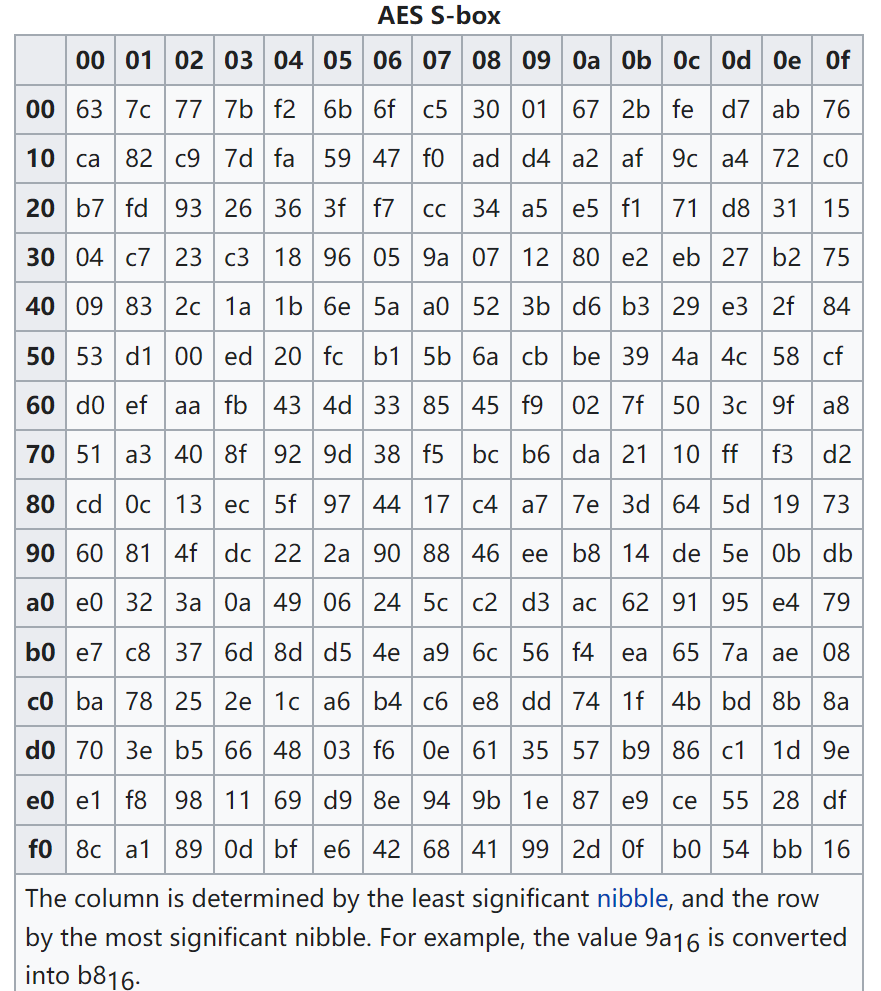
- Bytes substitution: a non-linear function 1 byte 1 byte. The S-Box is a 256-size table.
![14]()
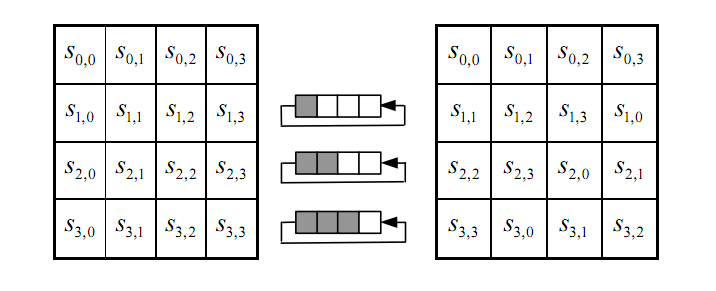
- Shift rows:
![15]()
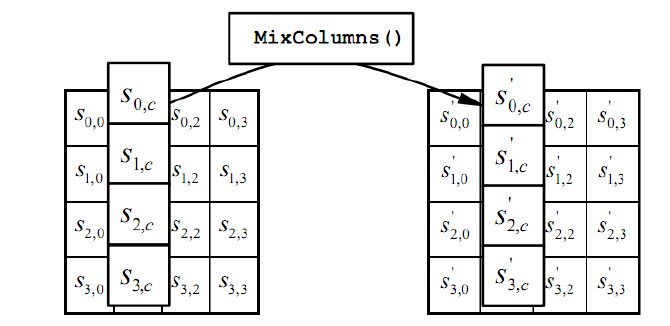
- Mix columns: the four bytes of each column of the state are combined using an invertible linear transformation.
for example:
![16]()
where the addition is XOR, multiplication is the multiplication of polynomials module , which is the minimal irreducible polynomial of degree 8.
Example:
[BK’09] Given pairs of input and output from 4 related keys in AES-256, can recover keys in time .
# Block ciphers from PRG
Can we build a PRF from a PRG ?
Let be a secure PRG , then Define 1-bit PRF :
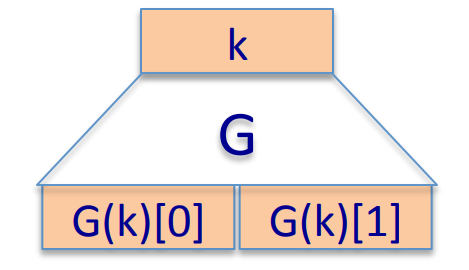
Theorem: if is a secure PRG , then is a secure PRF .
Similarly, we can construct n-bit PRF :
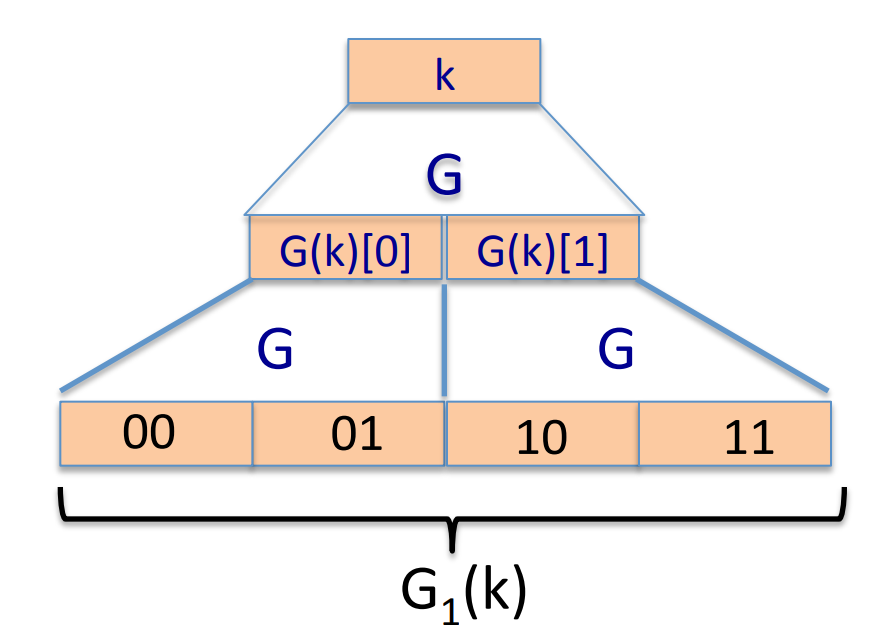
We can prove that is a secure PRF with the theorem given above:
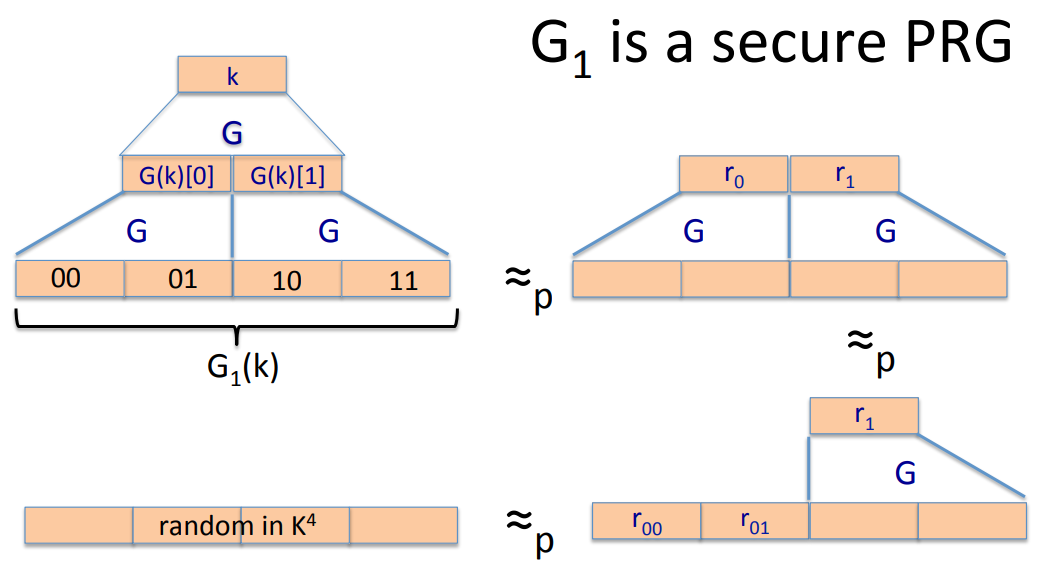
where stands for the real random number.
Lemma:We can build a secure PRP by a secure PRG with the Luby theorem and construction mentioned above.
# More discussion about PRF and PRP
Firstly we introduce the equivalent definition of secure PRF :

Let’s make a brief explaination.
- is fixed and the adversary don’t know.
- Adversary can make several queries to challenger, each query can be modified according to the response of the last query.
- For the query , if , then the challenger should randomly choose a , then respond to the adversary.
If , then the challenger should randomly choose a function and respond to the adversary. - After queries, the adversary will give the guess that or .
- EXP(0)=1 means that and the adversary guess . EXP(1)=1 means that and the adversary guess .
- Obviously, for a fixed adversary algorithm, due to the random choice of , the guess of adversary may vary. So we have the probability.
Similarly, we can define the secure PRP :

Noticing that the only difference is randomly choose in Permutations on .
- Example: all times algorithm have .
Lemma: Let be a PRP over , then for any q-qeury adversary , we have:
So if is large enough, then a secure PRP is also a secure PRF .
# Use block cipher: one time key
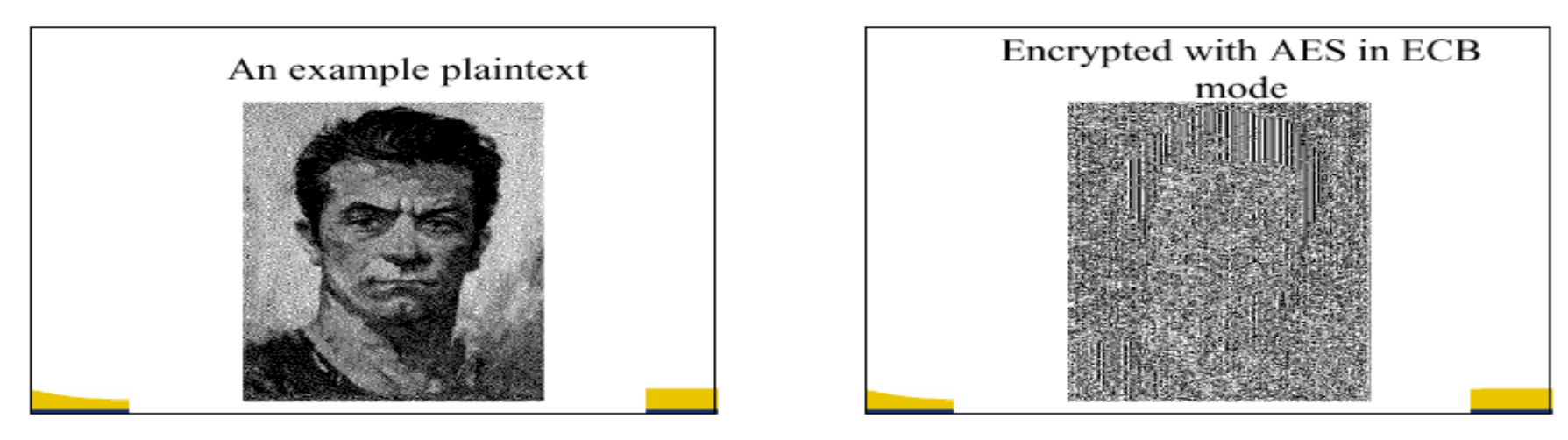
Don’t use the block cipher in Electronic Code Book( ECB ):
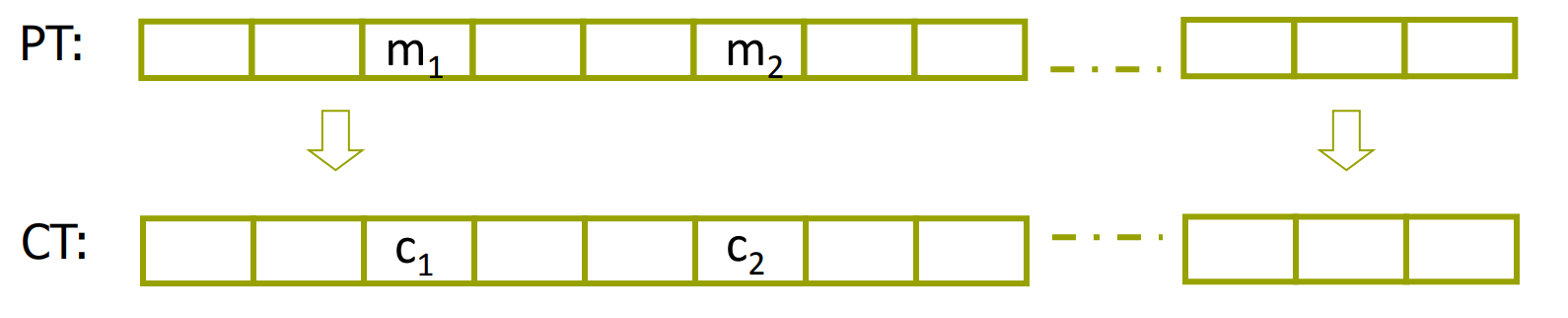
The problem is that if , then .
- Example:
![23]()
Then we can introduce the semantic security of the cipher:
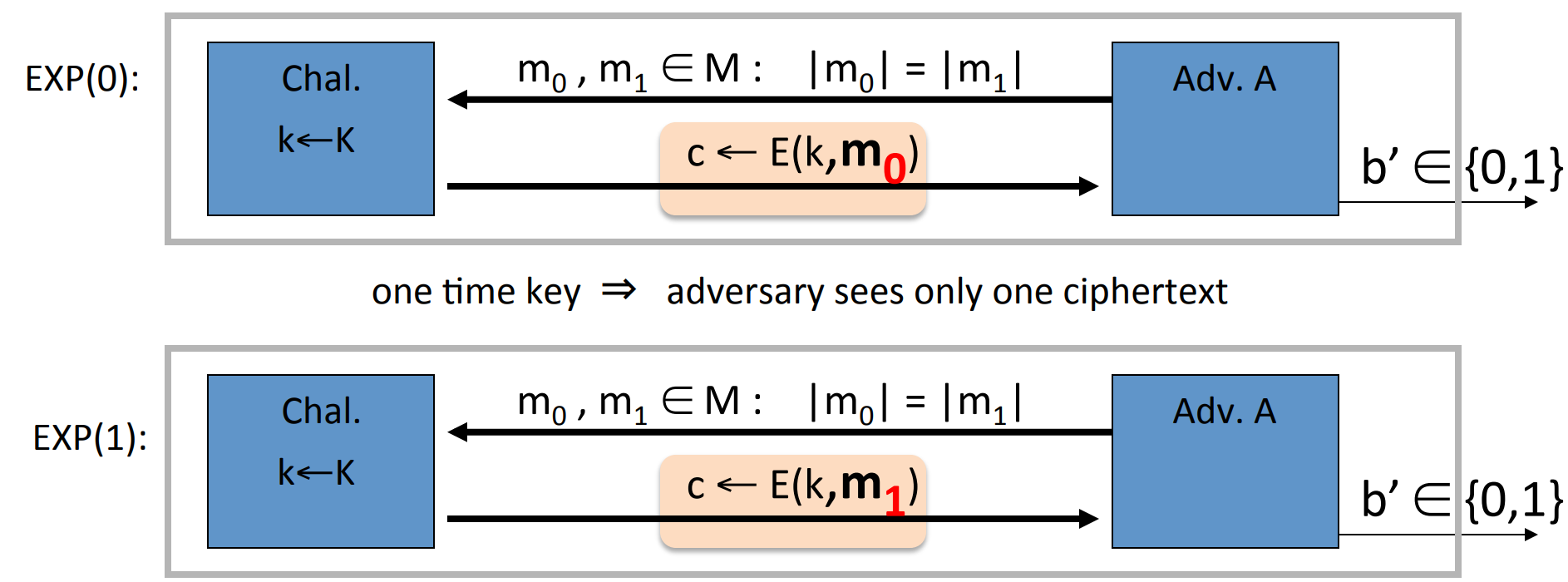
should be negligible.
Lemma: ECB is not semantic secure.
Proof: Construct an adversary such that:

then .
One secure construction is Deterministic counter mode from a secure PRF :
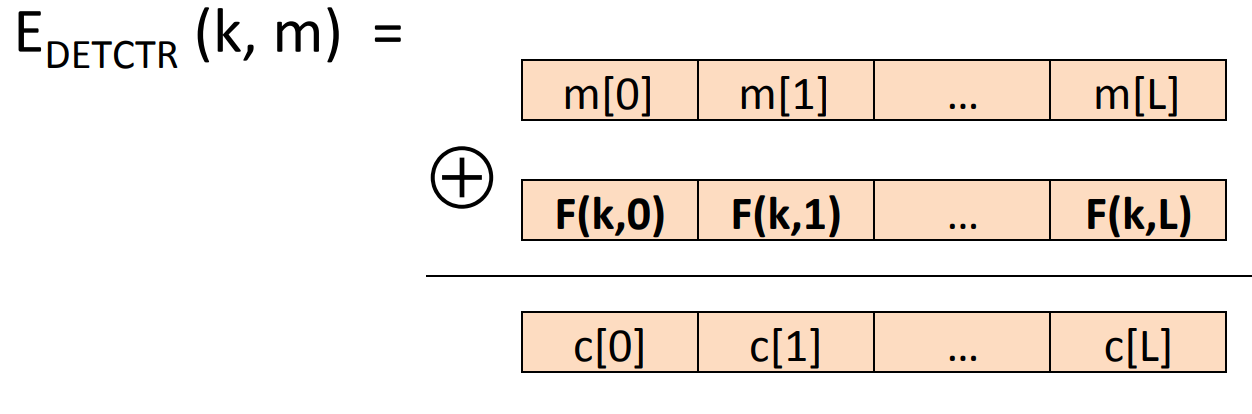
where .
Theorem: For any , if is a secure PRF over , then is a semantic secure cipher over .
In particularly, for any efficient adversary attacking , there exists an efficient PRF adversary such that:
# Use block cipher: many times key
Key used more than once adversary can see many CT s with same key.
Adversary’s power: Chosen Plain text Attack( CPA ):
- Adversary can choose a
PTand obtain itsCT.CPAis quite a conservative abstract of the reality.
Adversary’s goal: To break semantic security.
Since the adversary can choose PT , then we can introduce the semantic security over many-time key:

explaination:
- After the random choice of , is fixed for the queries.
- Adversary can modify query according to the response of the last query.
- If the adversary just want to know , then he can query with .
- Other stuff is similar to the previous definition.
- Example: if the key is used more than once, and for fixed , is always the same, then it is not semantic secure. We can construct:
![28]()
So we need to solve the problem that many-time key cipher is not semantic secure.
Solution 1: randomized encryption, where is a randomized function:
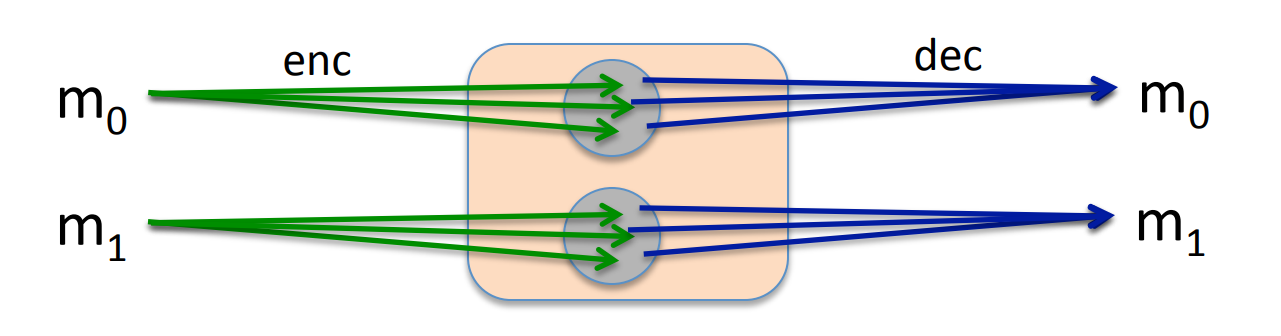
roughly speaking, CT -size= PT -size+#random bits.
Solution 2: nounce based encryption:
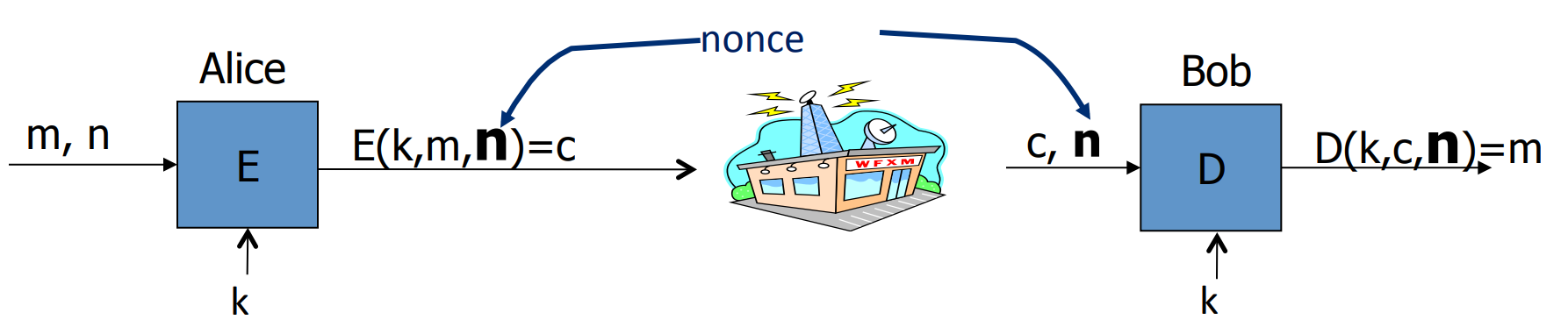
so that pairs are used only once.
# Use block cipher: Cipher Block Chaining( CBC )
Let be a PRP , then we can construct a chain of :
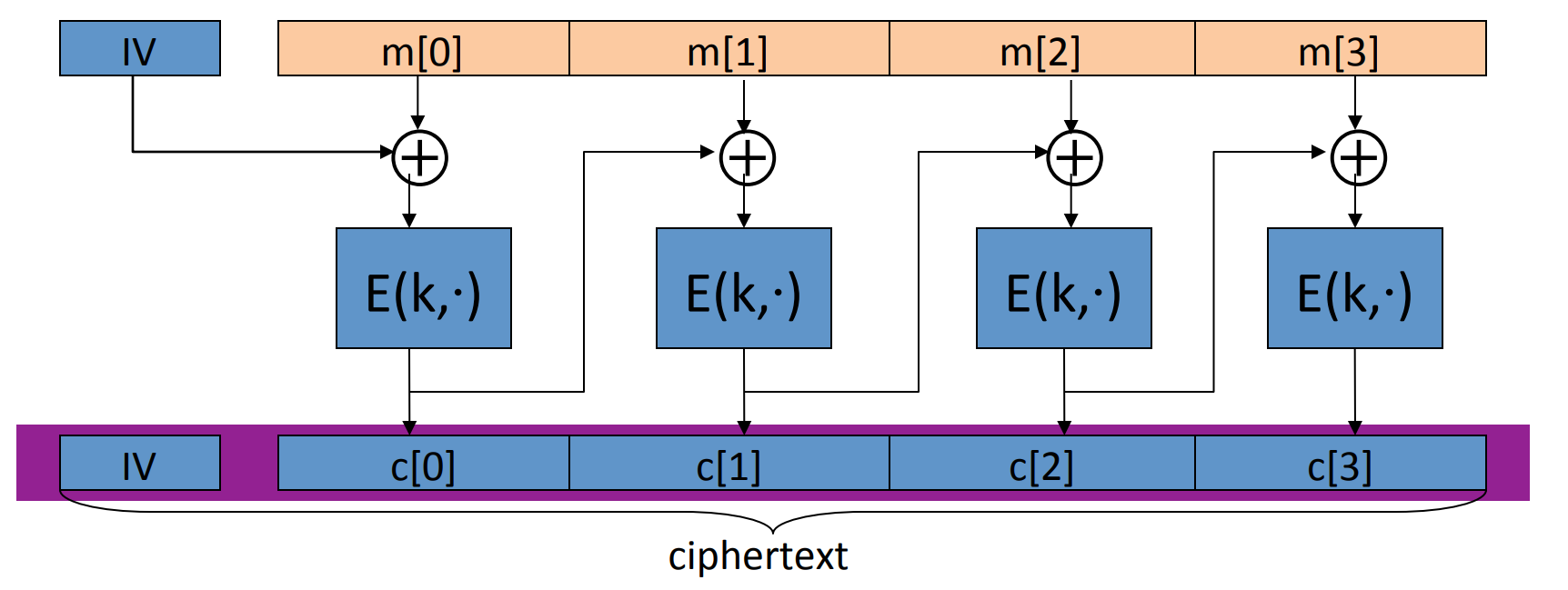
where IV stands for initial vector, and is chosen randomly in .
The decryption circuit is:
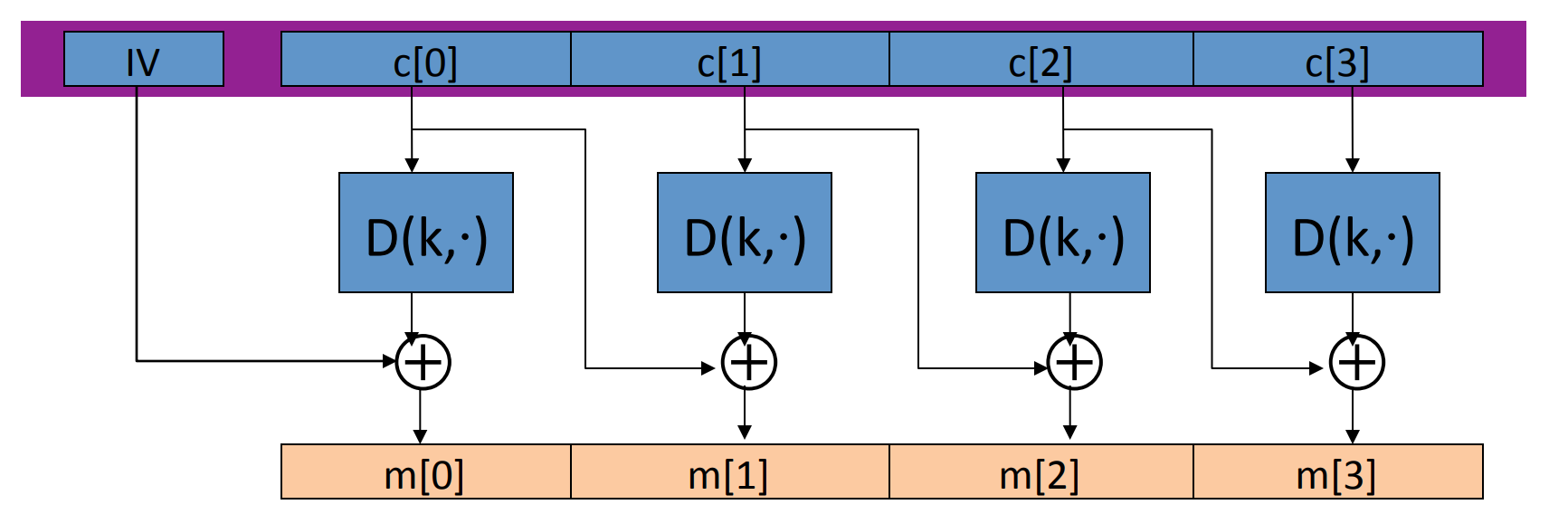
Theorem: If is a secure PRP over then is semantic secure under CPA over .
In particular, for a q-query adversary attacting ,there exists a PRP adversary such that
- Example, suppose we want , then for AES , we should guarantee . So after encrypting blocks, we should change the key.
for 3-DES, , so .
Warning: the IV must be chosen randomly each time of encryption!
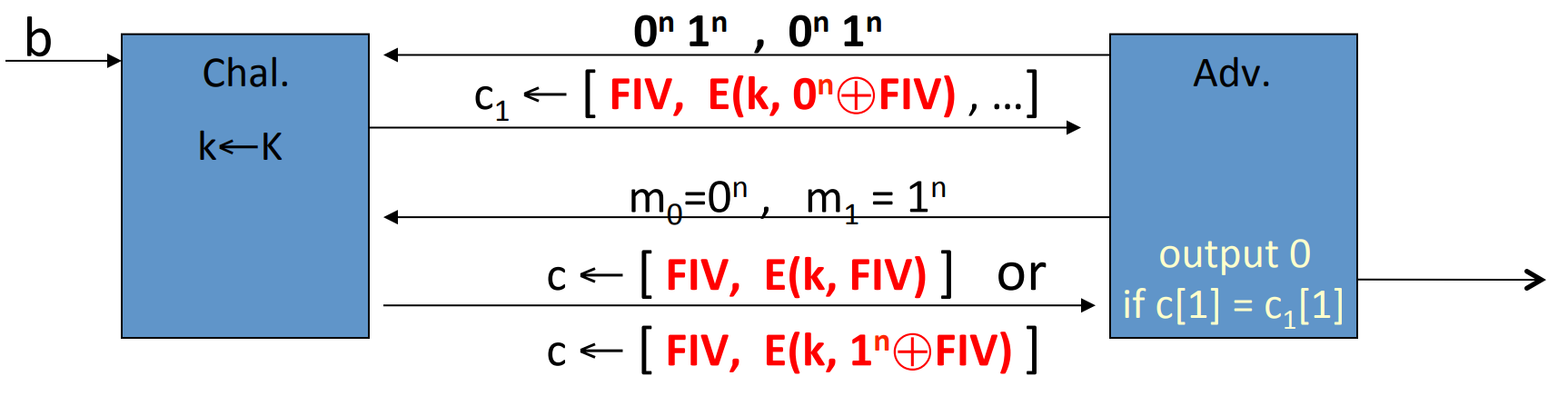
Lemma: CBC where attacker can predict IV is not CPA -secure.
Proof: if given IV0, then IV1 is predictable, then we can construct the adversary:

explaination:
- Since IV is in the head of
CTso the adversary can obtain IV. - Once obtained IV0, the attacker will predict IV1.
- The blue box is , which is the same
PTin the first query .
A obvious modification is that we won’t give the adversary IV, that is we encrypt IV into a nounce:
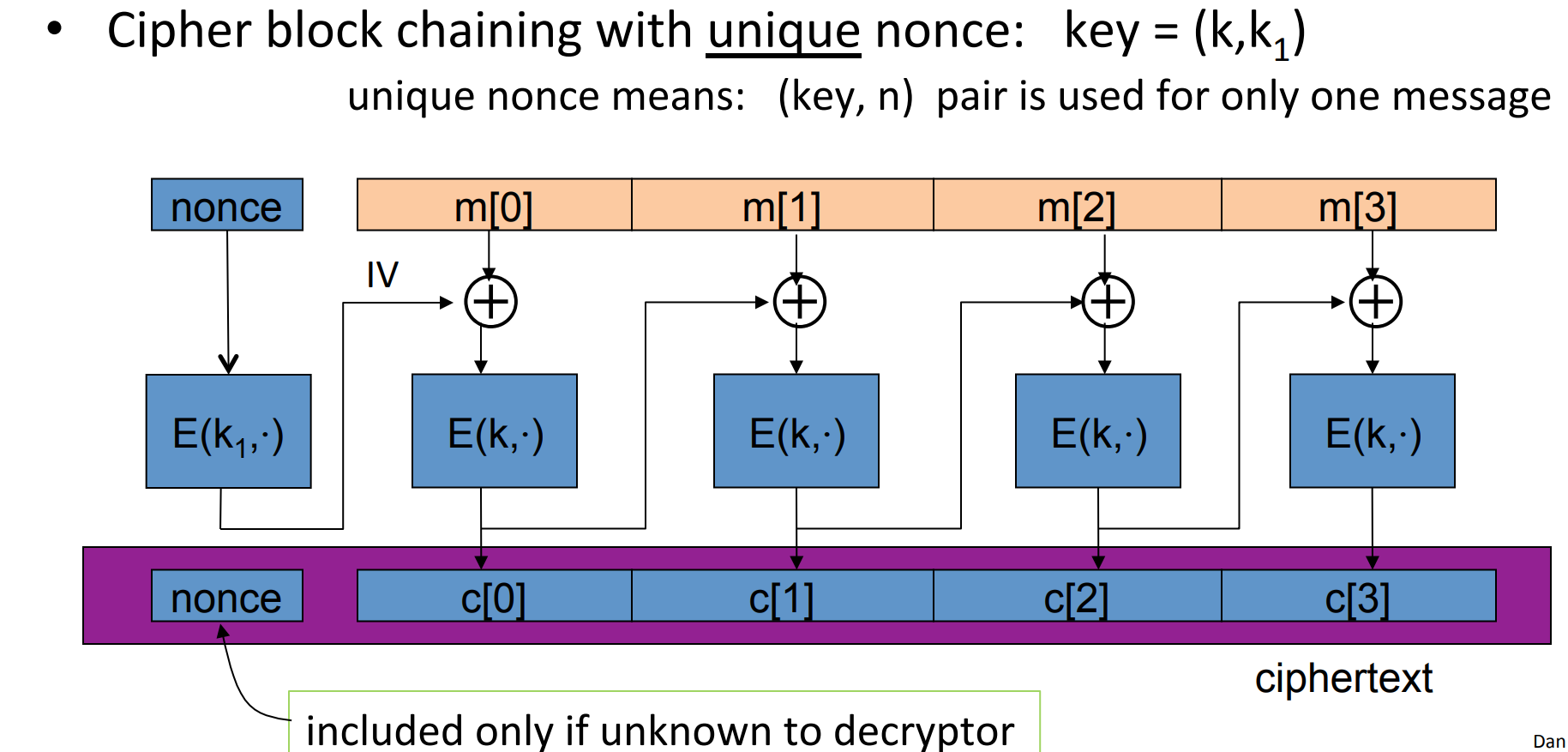
# Use block cipher: Counter Mode ( CTR )
Construction 1: rand CTR , randomly choose an Initial Vector(IV):
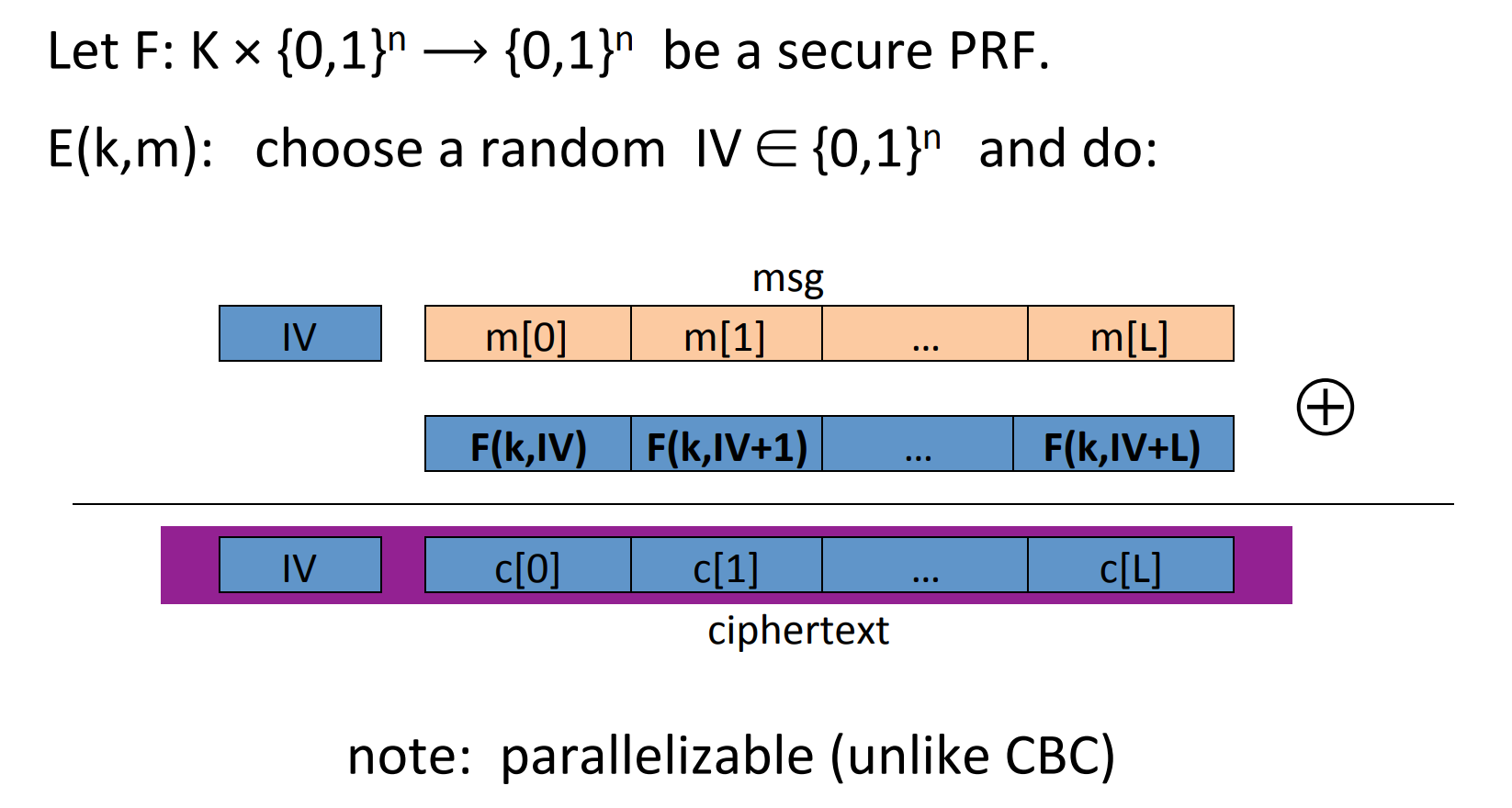
Construction 2: nounce CTR , we choose IV with counter:
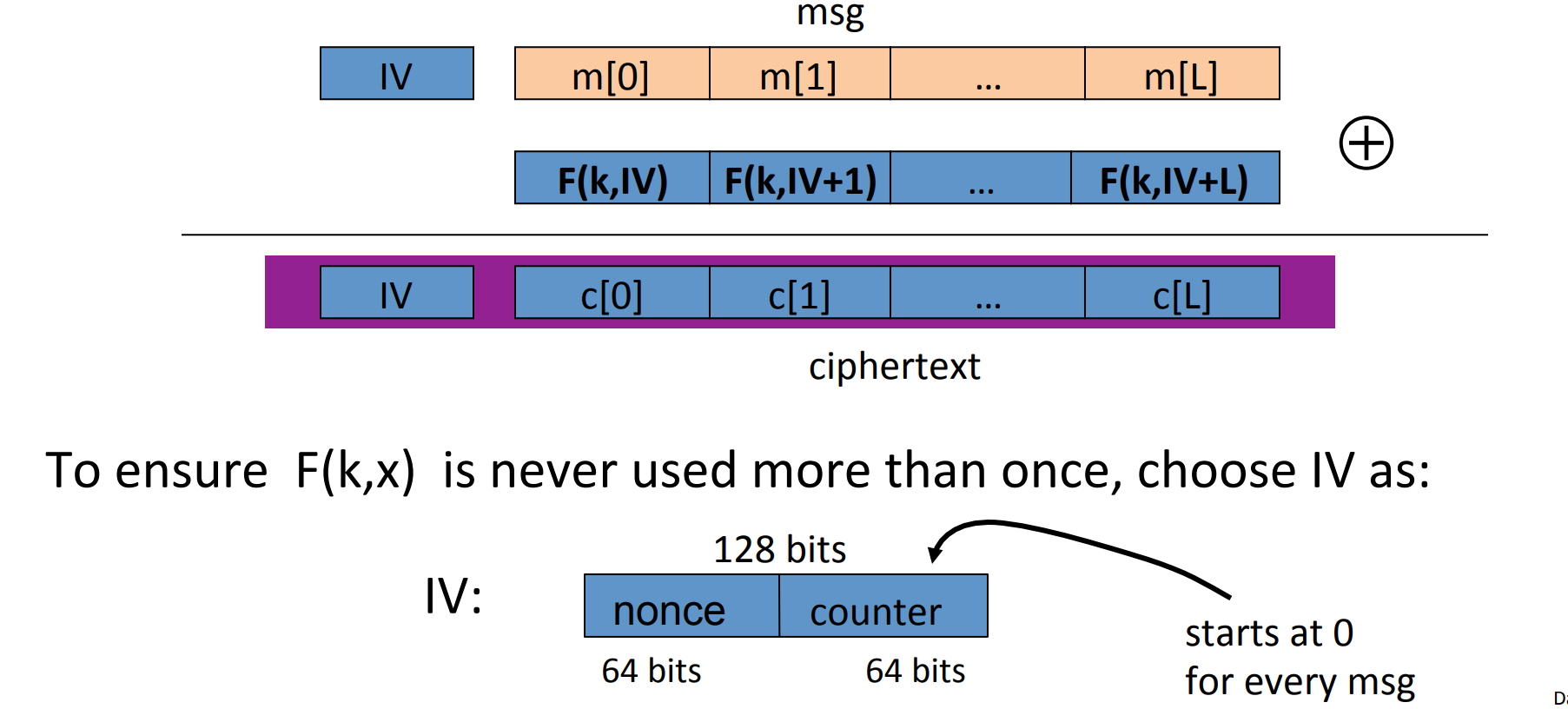
Theorem: If is a secure PRF over , then is semantic secure under CPA over .
In particular, for a q-query adversary attacking , there exists a PRF adversary such that
- Example: q=#messages encrypted with k, L=length of max messages, suppose we want , then for AES , we should guarantee . So after encrypting
CTs each len of , we must change the key.
Comparson: CTR vs. CBC :
| feature | CBC |
CTR |
|---|---|---|
| uses | PRP |
PRF |
| parallel processing | No | Yes |
| security | << | << |
# Message integrity
# Message Authentication Code( MAC )
The goal in this section is integrity while no confidentiality.
Definition: MAC defined over is a pair of algorithms:
- outputs .
- outputs ‘yes’ or ‘no’.
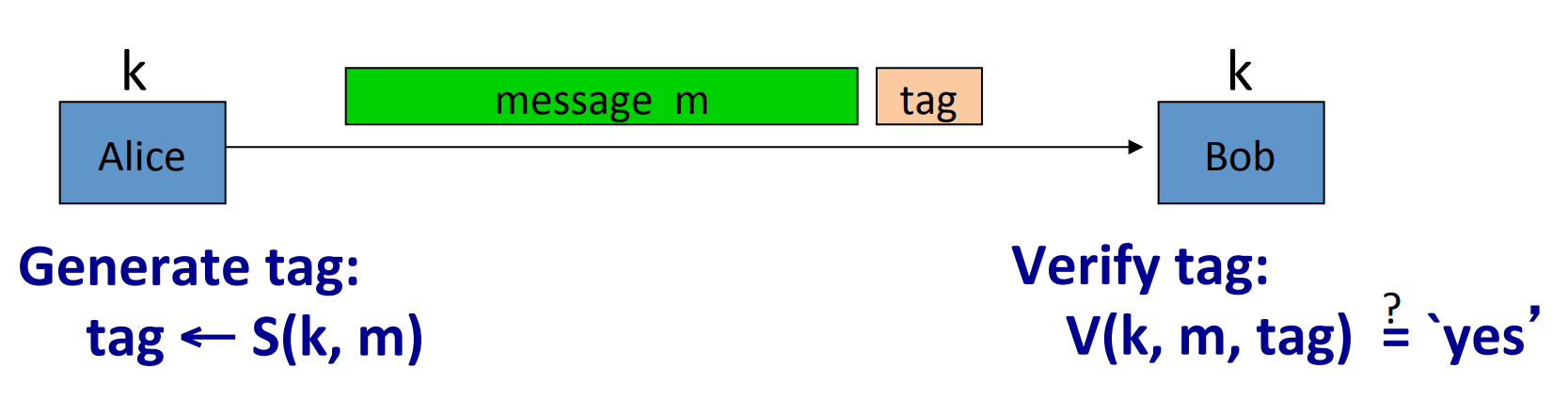
Let’s make a brief explaination. Alice uses message and generate function to generate a tag, and sends both message and tag to Bob. Bob uses the verification to verify if the message’s integrity.
- Example: generate function is , then the attacker could easily modify the message without being noticed.
The essence behind the example is that CRC is designed to detect random, but not malicious errors.
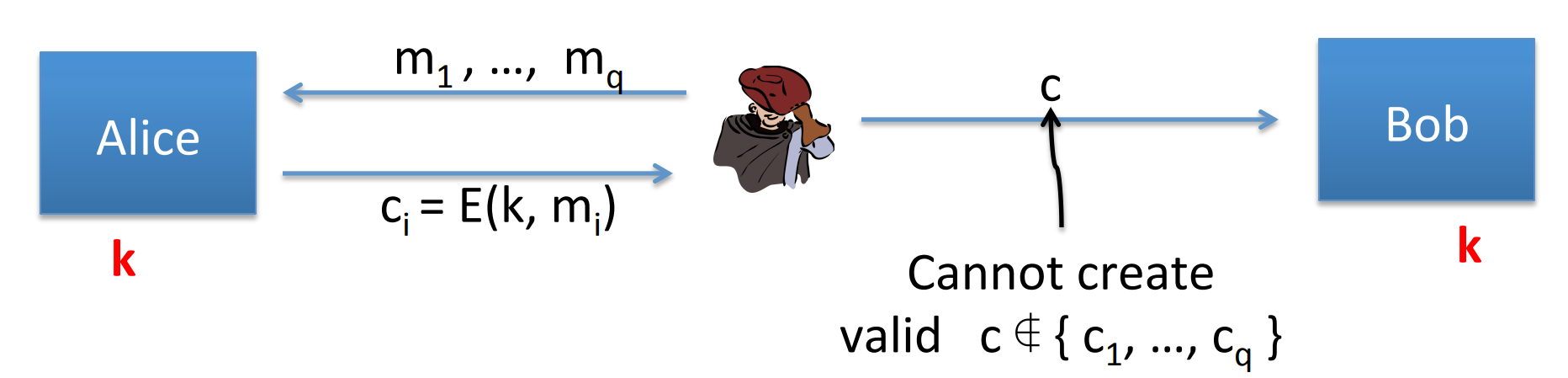
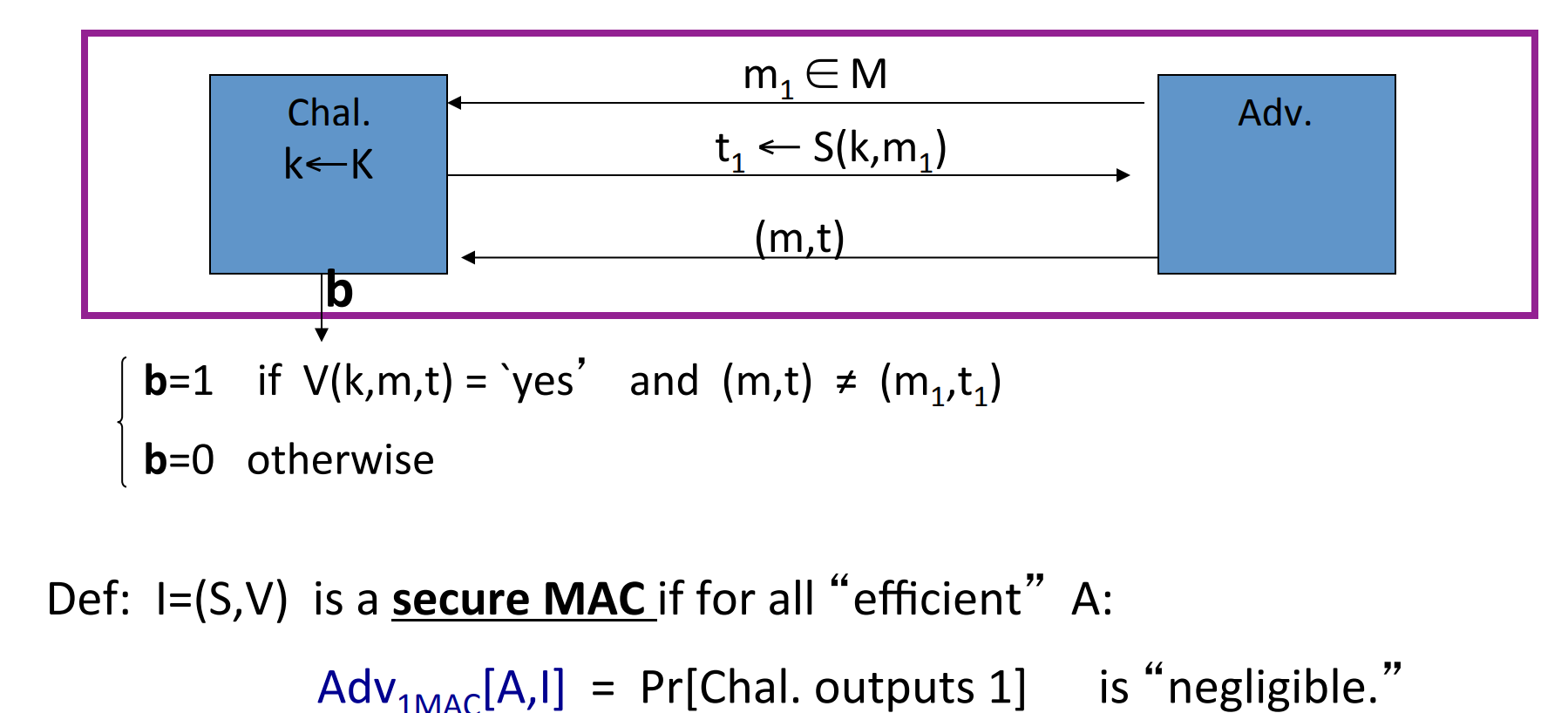
Let’s define a MAC game:
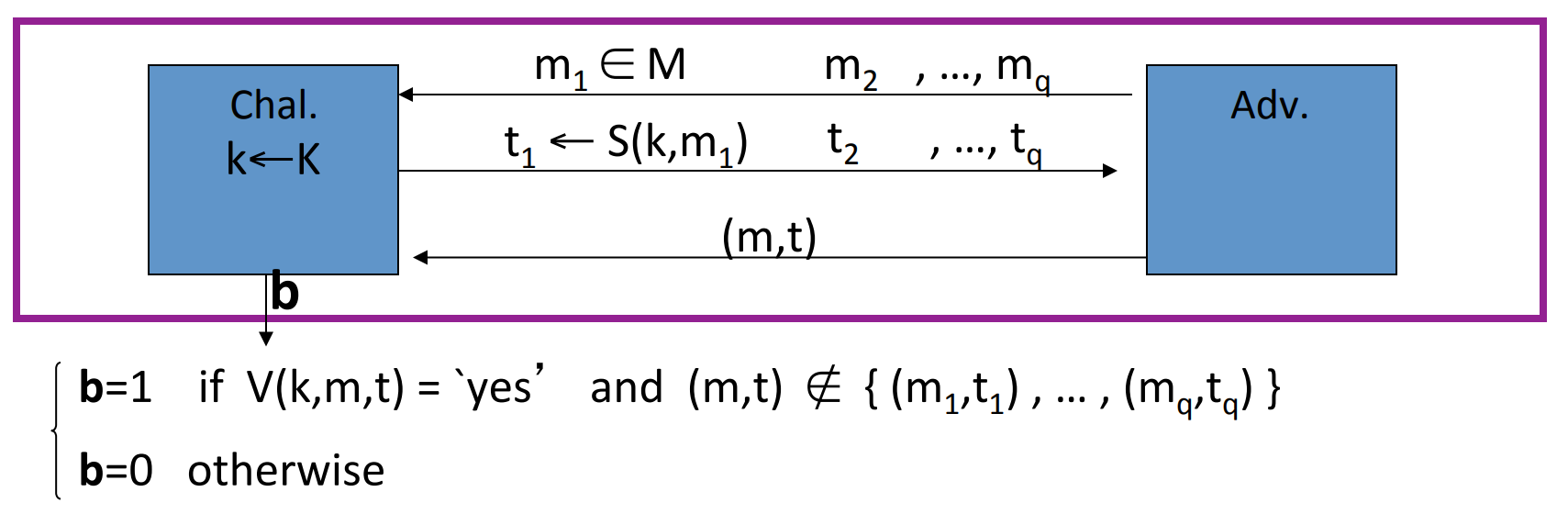
which means that the attacker’s power is Chosen Message Attack, he can choose and query several times, and the challenge would response the tag.
Then the attacker’s goal is to construct a pair of message and its corresponding tag not in the queries.
If the attacker can construct such a pair, then the MAC is not secure.
Definition: A MAC is a secure MAC if forall “efficient” adversary A:
is negligible.
- Example: In operating systems, every file and its filname is signed by a
MACto ensure the integrity of the file. So the virus can’t modify the file without being detected.
# MAC based on PRF
For a PRF , we can construct a MAC :
- .
- : outputs ‘yes’ if and ‘no’ otherwise.
notice that when is too small, then the attacker can guess the tag easily.
Theorem: If is a secure PRF and is negligible, then constructed as above is a secure MAC .
In particular, for every efficient adversary attacking , there exists an efficient PRT adversary such that:
Proof:
- Example: AES, A
MACfor 16-byte messages.
How to convert small MAC to big MAC ? We just need to convert small PRF to big PRF . Methods:
- CBC-MAC
- HMAC
# CBC-MAC and NMAC
Construction 1. encrypted CBC-MAC :
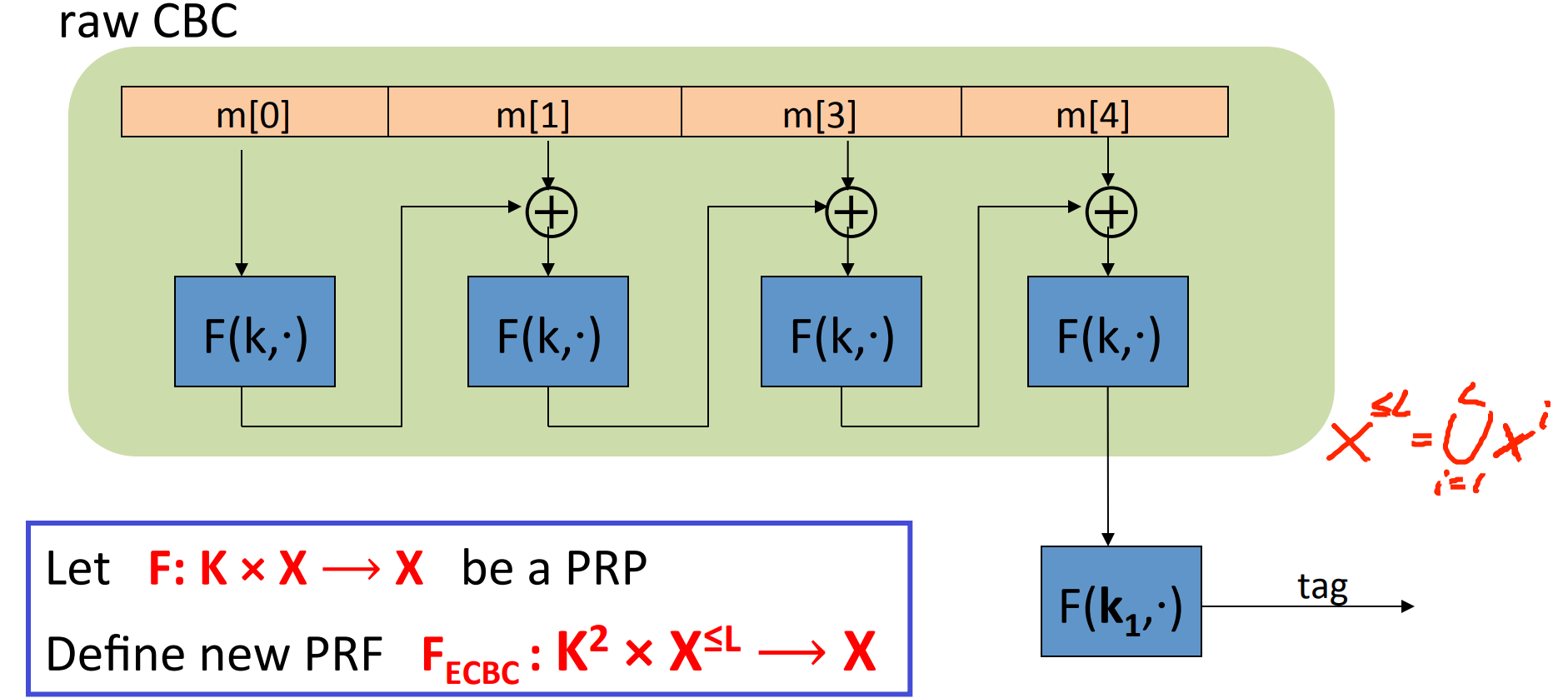
where .
Let be a PRF , then the construction above defines .
Construction 2. NMAC (nested MAC)
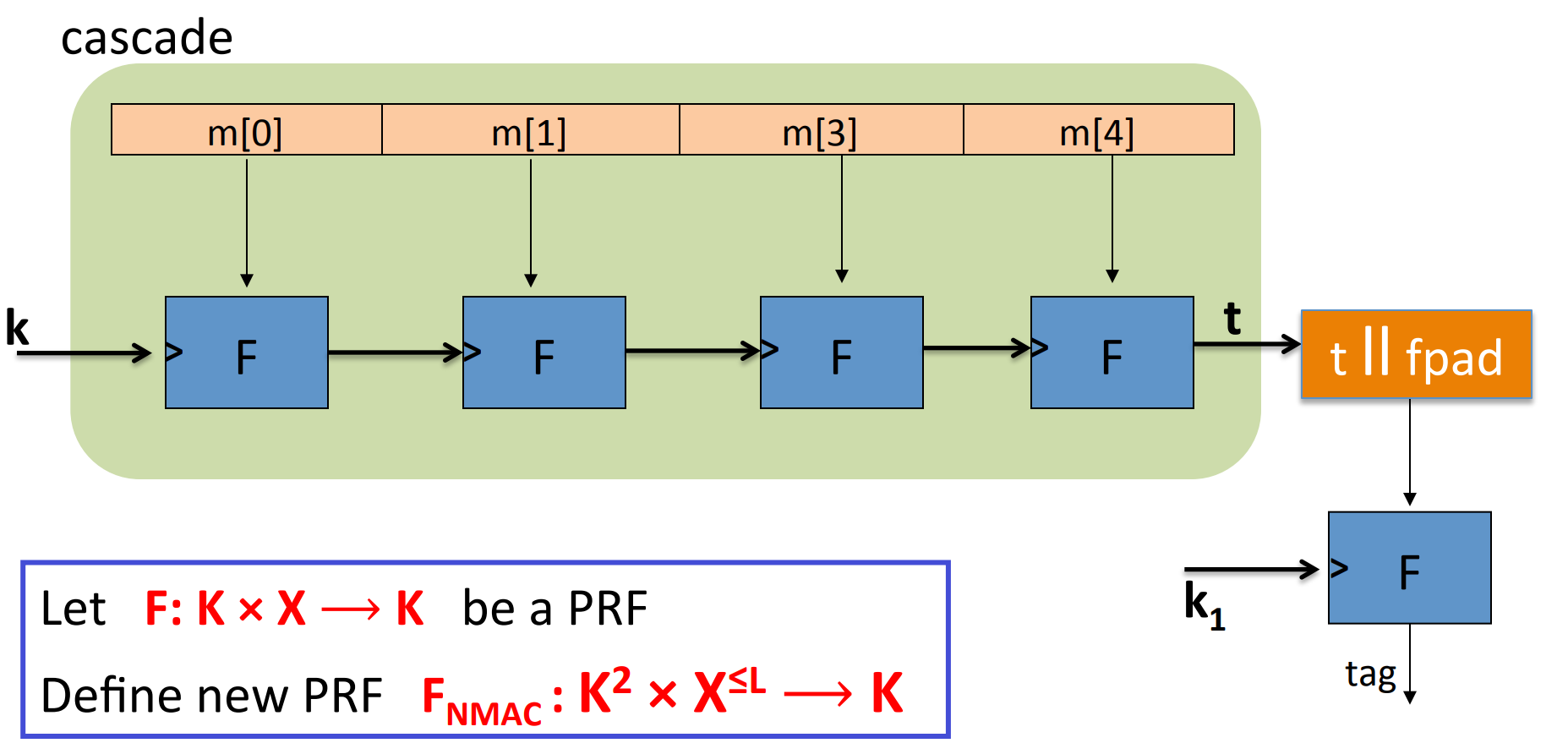
Let’s consider why the last encryption step in CBC-MAC is necessary?
Suppose we just define , where .
Then could be easily broken by chosen message attack:
- Choose an arbitrary one-block message .
- Request tag for , get .
- Ouput put t as MAC forgery for the two-block message . since:
so tag and message can be constructed and verified.
Theorem: For any , for every efficient q-query PRF adversary attacking or , there exists an efficient adversary such that:
CBC-MACis secure as long as .NMACis secure as long as .
- Example: For AES, if we want , then , since , so after messages must change the key.
Let’s see an attack when the key is not changed.
It’s easy to prove that ECBC and NMAC have the extension property:
let be a big PRF that has the extension property, then we can attack it as following:
- Issue messages queries randomly, and obtain responses .
- We can find collision with high probability, according to the birthday paradox.
- Choose arbitrary and query for .
- Output .
So a better rand construct is Rand CBC RCBC :
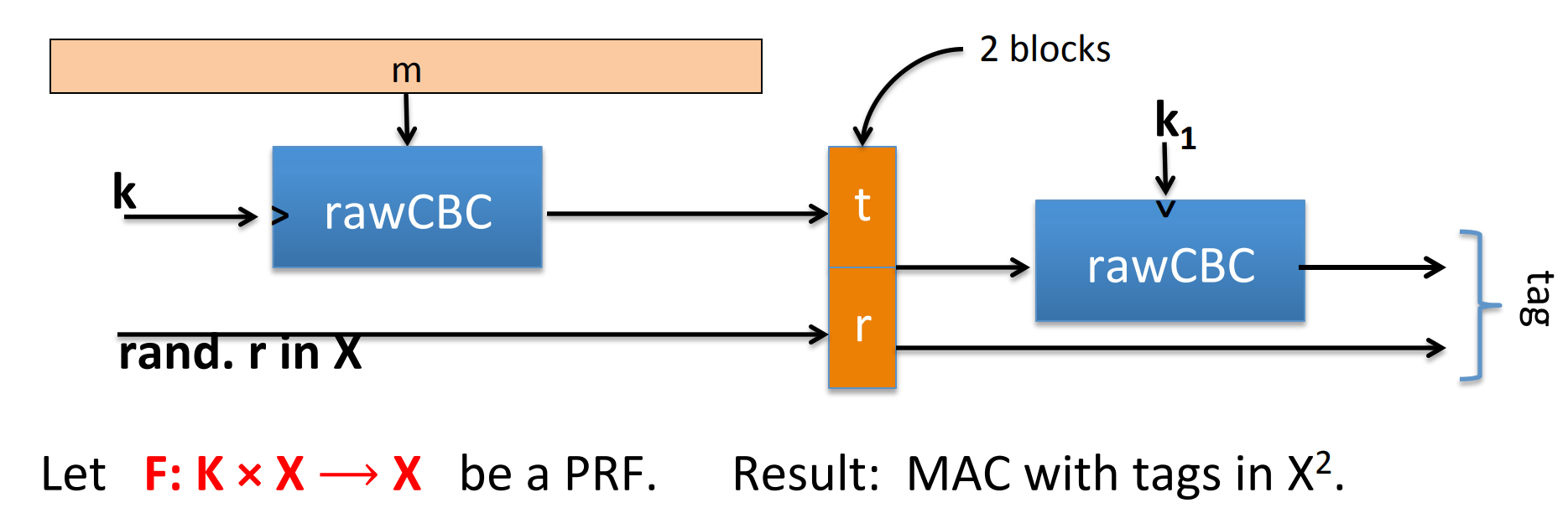
Security is:
Comparison between ECBC and NMAC :
ECBCis commonly used as an AES-basedMAC. e.g. CCM encryption mode(used in 802.11i).NMACnot usually used withAESor3DES, the main reason is that it changes the key on every block, so it needs to do the key expansion several times.
# MAC padding
When MAC (e.g. constructed by ECBC )'s message length is not a multiple of block size, we need to pad the message.
Construction 1.
Padding with all 0s.
Then the MAC becomes insecure in that the attacker can obtain the tag of then output , since
For security, padding must be invertible, and secure:
Construction 2. (ISO)
Pad with “100…00” and Add new block if needed.
- Example, if block size = 8, then , .
Obviouly the padding strategy is invertible since one can remove several 0s until a single 1, then get the original message. It is secure as well.
Construction 3. (CMAC NIST standard)
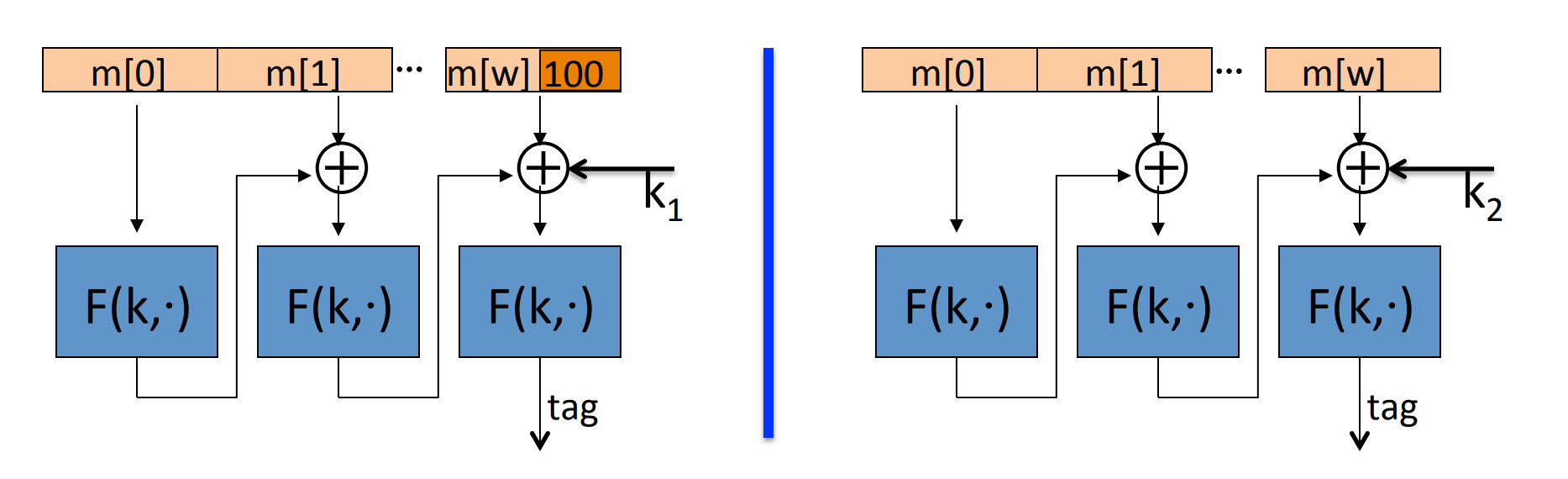
key = , if we need padding then use the left circuit, otherwise use the right one.
- No final encrypton step, since extension attack is thwarted by last key xor.
- No dummy block, since we separate the cases with two different keys.
# PMAC and Carter-Wegman MAC
ECBC and NMAC are sequential, can we build a parallel MAC from a small PRF ?
Of course, it is named PMAC (Parallel MAC):
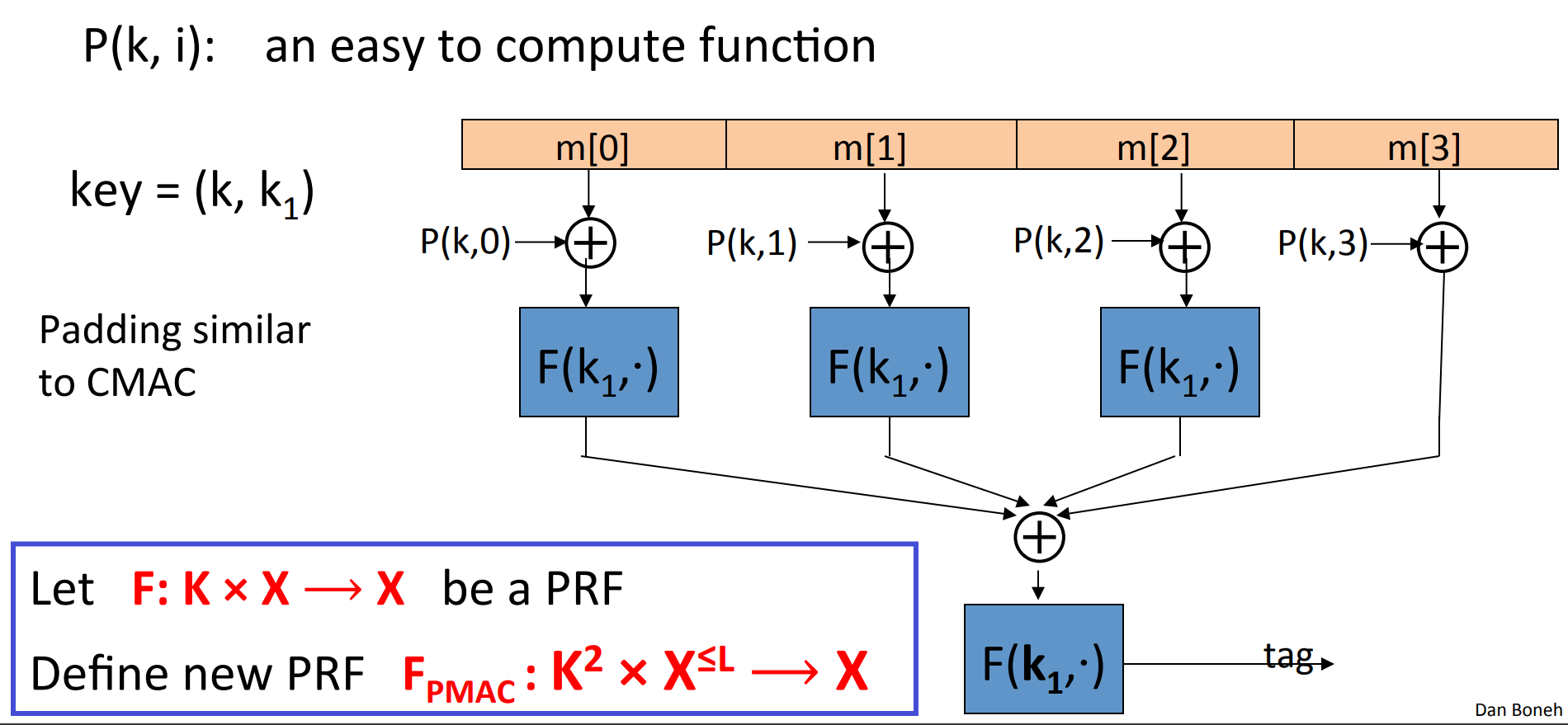
the function here is used to encrypt sequence, to avoid swap attack. Without , the attacker could swap two blocks and get the same tag.
Theorem: For any , If is a secure PRF over then is a secure PRF over .
In particular, for any efficient q-query PRF adversary attacking , there exists an adversary such that:
If only one block of PMAC is changed, then the tag can be re-computed quickly.
One time MAC is another kind of MAC not based on PRF .
If the key is changed on every message like OTP , then the attacking game could be defined as:
so the attacker could only query 1 message.
- Example, one time
MAC:- let be a large prime (e.g. )
- , two random int in .
- where each block is 128 bit int.
where
is a polynomial of degree .
Theorem: the one-time MAC in the last example, we have:
So basicly given the adversary has no info about .
By one time MAC we can construct many-time MAC with high speed:
Let be a secure one-time MAC over .
Let be a secure PRF .
Carter-Wegmen MAC :
for random .
So given , we can run the verification function as:
Theorem: If is a secure one time MAC and is a secure PRF then CW is a secure MAC outputting tags in .
# Collision resistance
# Introduction
So far, four MAC constructions:

Definition: Let be a hash function (),
A collision for is a pair such that:
A function is collision resistant if for all explicit efficient ,
is negligible.
Let be a MAC for short messages over (e.g. AES ).
Let .
Then we can construct a MAC :
Theorem: If is a secure MAC and is collision resistant then is a secure MAC
Suppose is not resistant, and the attacker can obtain collision . Then after quering the tag for , the attacker can output since .
# Generic birthday attack
Theorem (birthday paradox): Let be independent identically distributed integers. Then when then .
Proof: we only prove when are all subject to uniform distribution (it’s the worst case):
So a generic attack is randomly choose elements in , then with a high probabilty that we can find a collision. .
# The Merkle-Damgard Paradigm
Given a CR (collision resistant) hash function for short messages, we can construct CR hash function for long messages. That is Merkle-Damgard iterated construction:
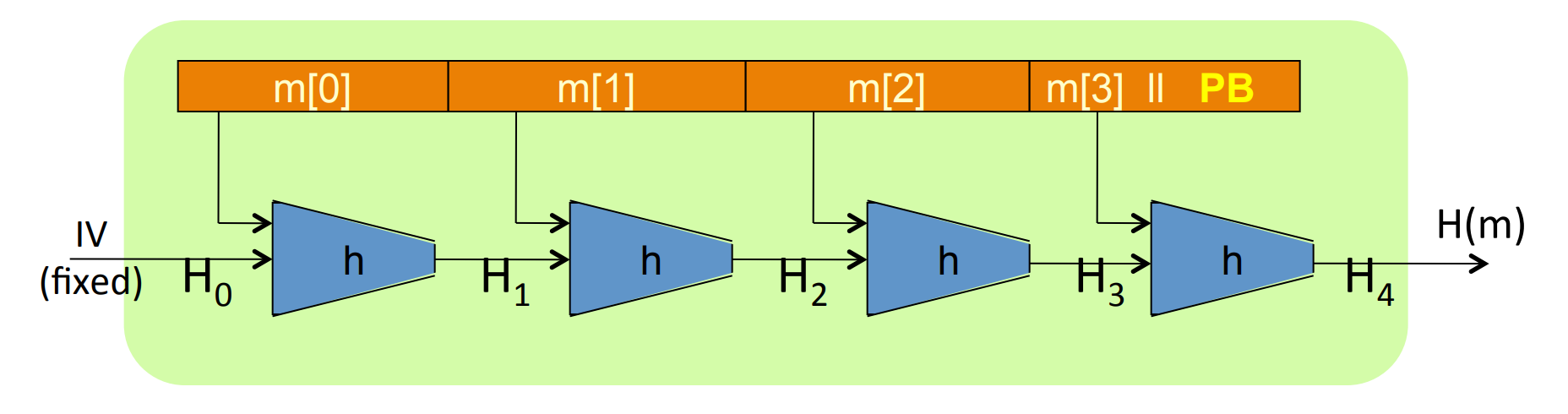
Give , we obtain .
We say is compression function and is the chaining variables (the output of each ).
Padding block:

if no space for at least 65-bits padding block, then add another block.
Theorem: If is collision resistant, then so is in Merkle-Damgard paradigm.
Proof: We prove collision on collision on .
Suppose , then we consider the chaining variables:
And we have
If or or , then we obtain a collision for .
Otherwise, we have , we can repeat the process above, since (collision for ), then at least can we find , then the collision for is found.
QED.
# Constructing compression functions
Suppose is a block cipher, then the Davies-Meyer compression function is:
Theorem: Suppose is an ideal cipher (is a collection of random permutations), then finding a collision takes evaluations of , and it’s the best cost possible.
And there are other compression functions based on block cipher:
- Miyaguchi-Preneel: , and the hash function “Whirlpool” is constructed by this compression function.
- , this one is insecure!
# HMAC : a MAC from SHA-256
We now talk about MAC from a Merkle-Damgard hash function.
If is a collision resistant hash function, then we construct MAC with it.
Construction 1.
This one is insecure! Since Merkle-Damgard iteration has the extension property, so given , we can compute for any .
Construction 2. Standardized method: HMAC (Hash-MAC)
where ipad and opad are consts defined previously.
It’s quite similar to NMAC :
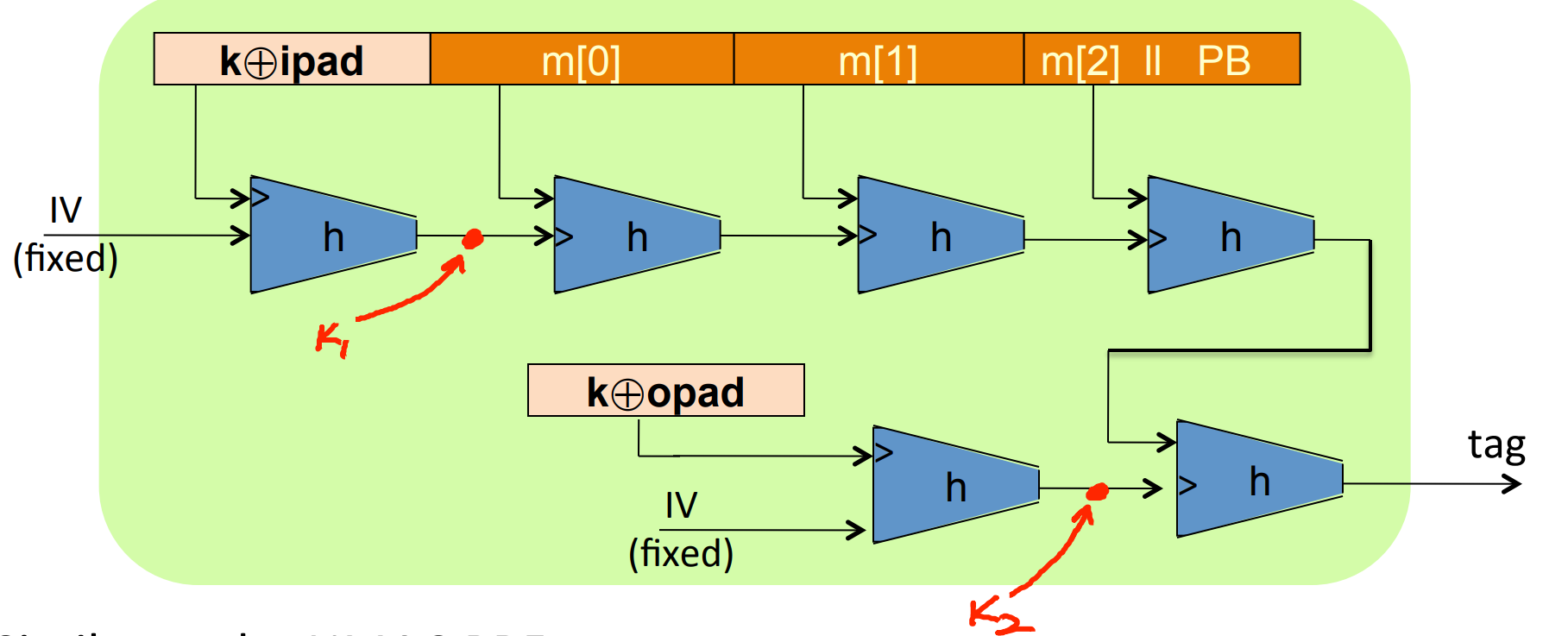
if we view the output as the input two keys for NMAC . However, in HMAC , and are not independent.
HMAC is assumed to be a secure PRF , secure bounds are similar to NMAC – need to be negligible.
# Timing attack on MAC verification
In the process of verification, if we need to compare two strings, actually it’s comparing chars one by one, and return immediately if find a inequality.
So there is a timing attacking strategy:
- Query server with the message and a random byte.
- Loop over all possible first byte of tag, and query server. If it takes a little longer time to respond than step 1, then we find the right first byte tag for the message.
- Repeat the process to find other bytes of the tag.
Defense:
instread of:
1 |
|
we use:
1 |
|
So the attacker would not know the values being compared.
# Authenticated Encryption
# Active attacks on CPA-secure encryption
In this module, we talk about encryption against tampering, to ensure both confidentiality and integrity.
Without integrity, the confidentiality is vunable to active attacks.
- Example: In IP packet, the attacker could just modify the beginning:
![50]()
then the server will “help” to decrypt the packet and send it to the attacker. In this case, the lack of integrity causes the confidentiality to be vunable to active attacks.
We can conclude lessons:
CPAsecurity cannot guarantee secrecy under active attack.
We use only two modes:
- If message needs integrity while no confidentiality, use a
MAC. - If message needs both integrity and confidentiality, use
authenticated encryption(this module).
# Definition
Definition: An authenticated encryotion system is a cipher where
where is the space of nounce, and is optional. stands for the state that the cipher text is rejected.
The system is supposed to provide semantic secure under a CPA attack and ciphertext integrity. CPA attack is introduced before, it means that the attacker should not be able to distinguish two experiments by just querying several .
While for ciphertext integrity, it’s natural that the attacker should not construct a ciphertext that is accepted:

has ciphertext integrity if forall efficient ,
is negligible.
Definition: cipher has authenticated encryption ( AE ) if:
- semantically secure under
CPA. - has ciphertext integrity.
- Example:
CBCwith randIVdoes not provideAE, since it never outputs so the integrity is not guaranteed.
If the AE is guaranteed, what intuition can we get?
- authenticity, which means that the attacker could not fool Bob into thinking a message is sent from Alice:
![52]()
- Security against
CPA.
# Chosen ciphertext attacks ( CCA )
Adversary’s Power: both CPA and CCA :
- Can obtain the encryption of arbitrary messages of his choice.
- Can decrypt any ciphertext of his choice, other than chosen plaintext.
Again, this is quite a conservative modeling of real life.
A more formal definition is as following:
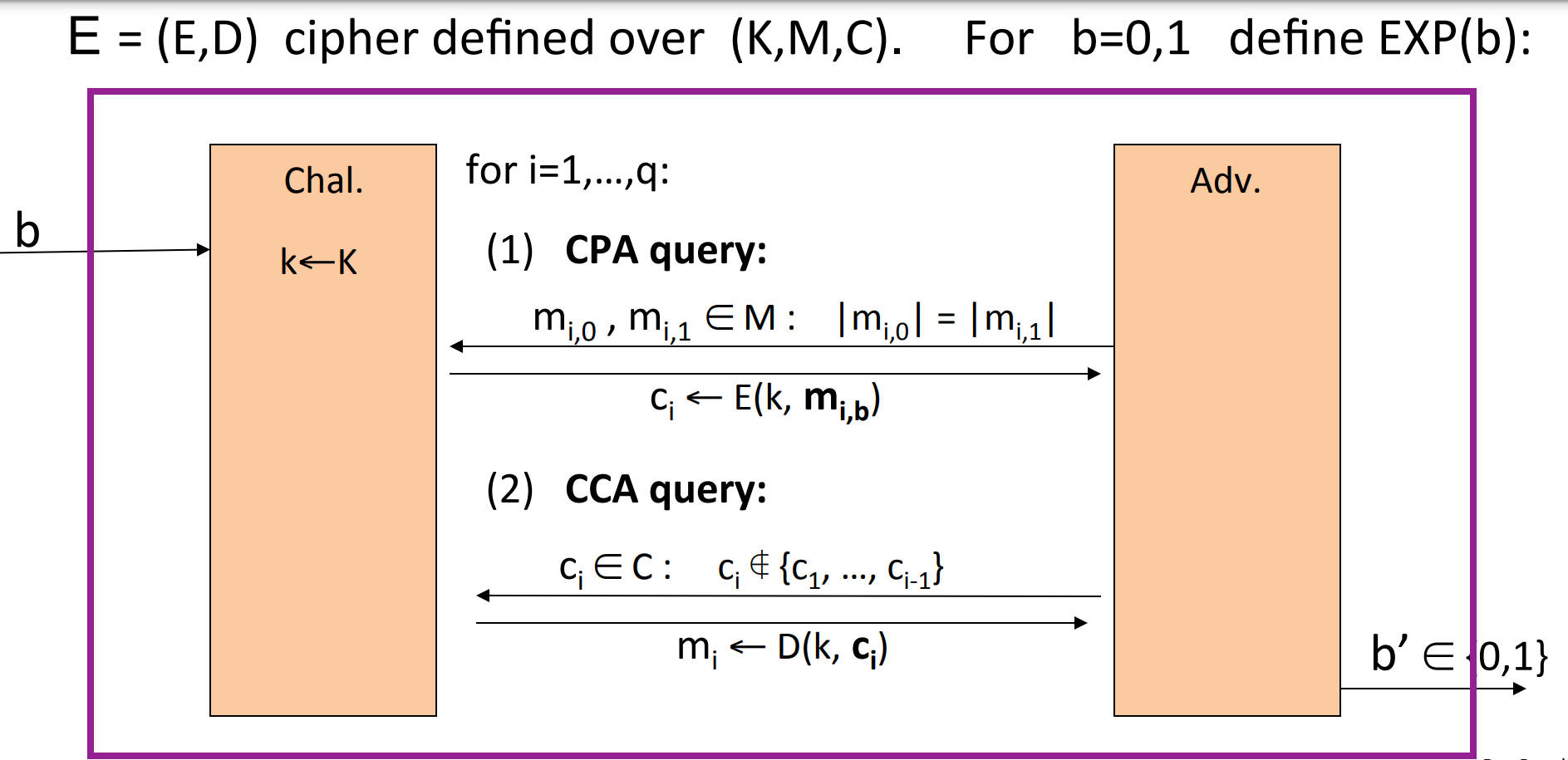
is CCA secure if for all efficient :
is negligible.
- Example:
CBCwith randomIVis notCCAsecure.
The attacker could first do theCPAwith two 1-block messages , and get . Then the attacker can useCCA, to query the decryption of , the decryption is , then the attacker can learn .
Theorem: Let be a cipher that provides AE . then is CCA secure.
In particular, for any q-query efficient , there exists efficient such that:
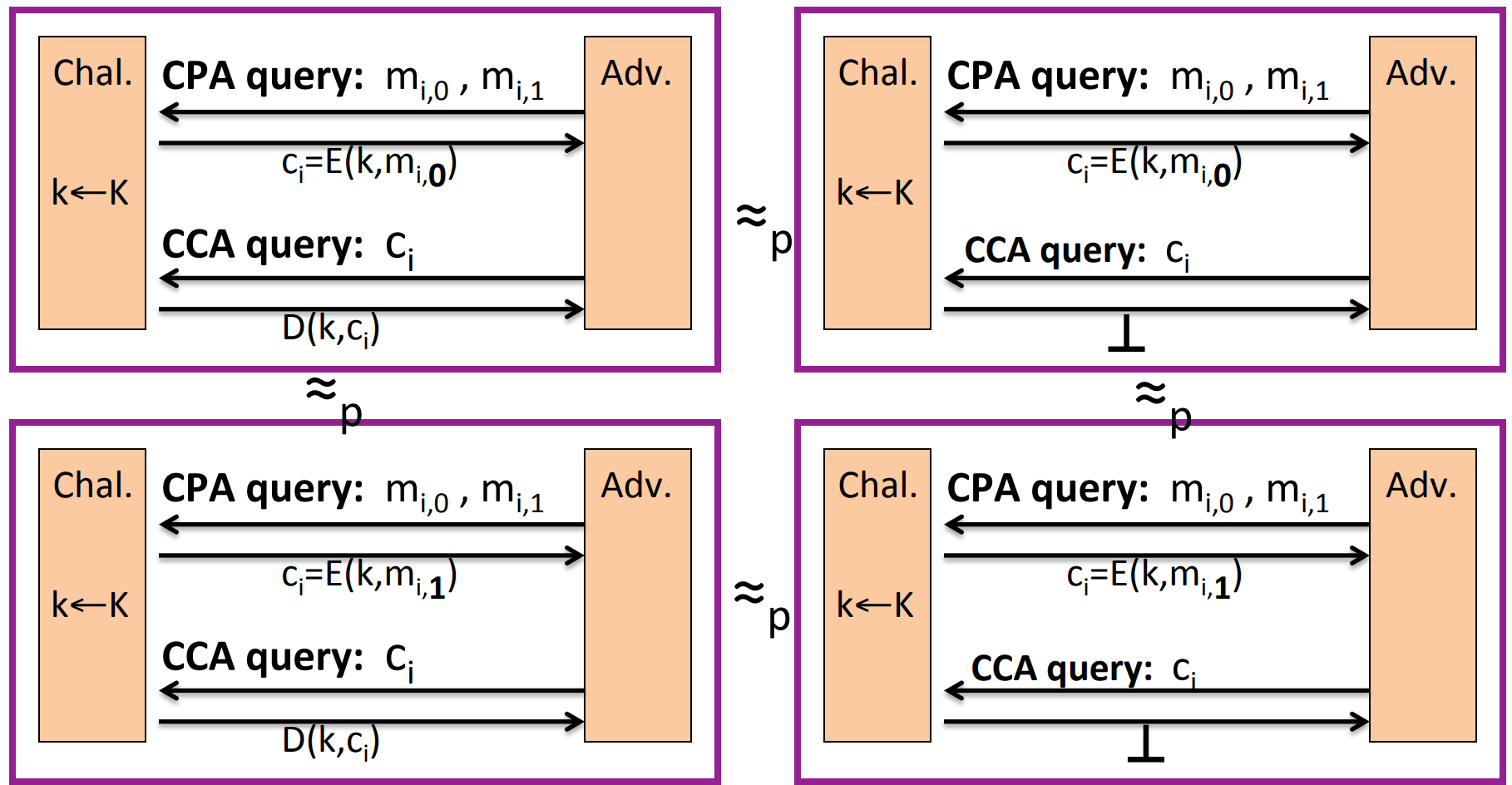
Proof sketch:
Step 1. Since AE guarantees ciphertext integrity ( CI ), then the attacker shouldn’t be able to construct any acceptable ciphertext other than ones he challenged. So it would be indinstinguishable thath the challenger always outputs in CCA queries:
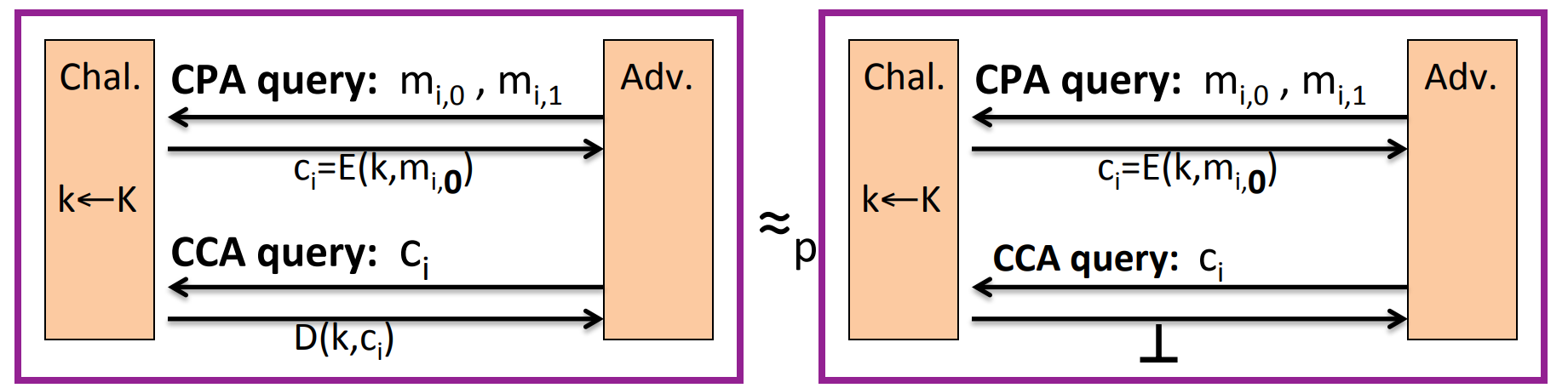
Step 2. Since the challenger always outputs , then the CCA queries is useless, we can ignore it. And because AE guarantees CPA security, then it’s indistinguishable that the response to CPA query is or :
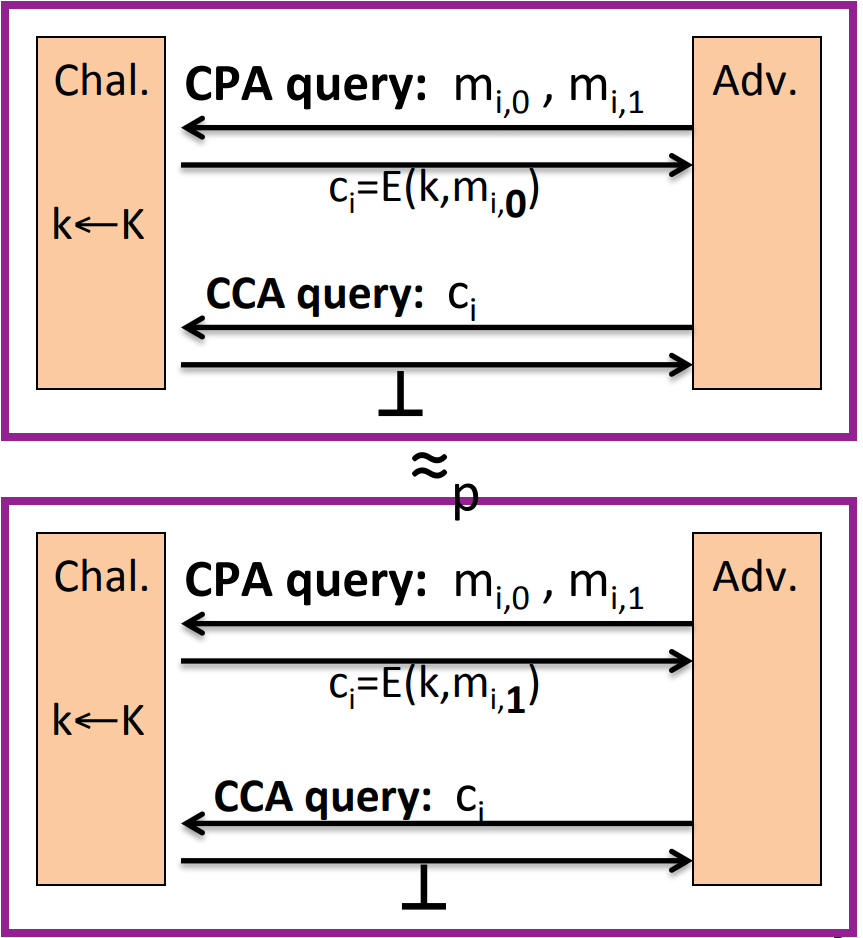
Step 3. Similar to step 1, we can get back to CCA queries. So as a whole:
# Constructions from ciphers and MAC
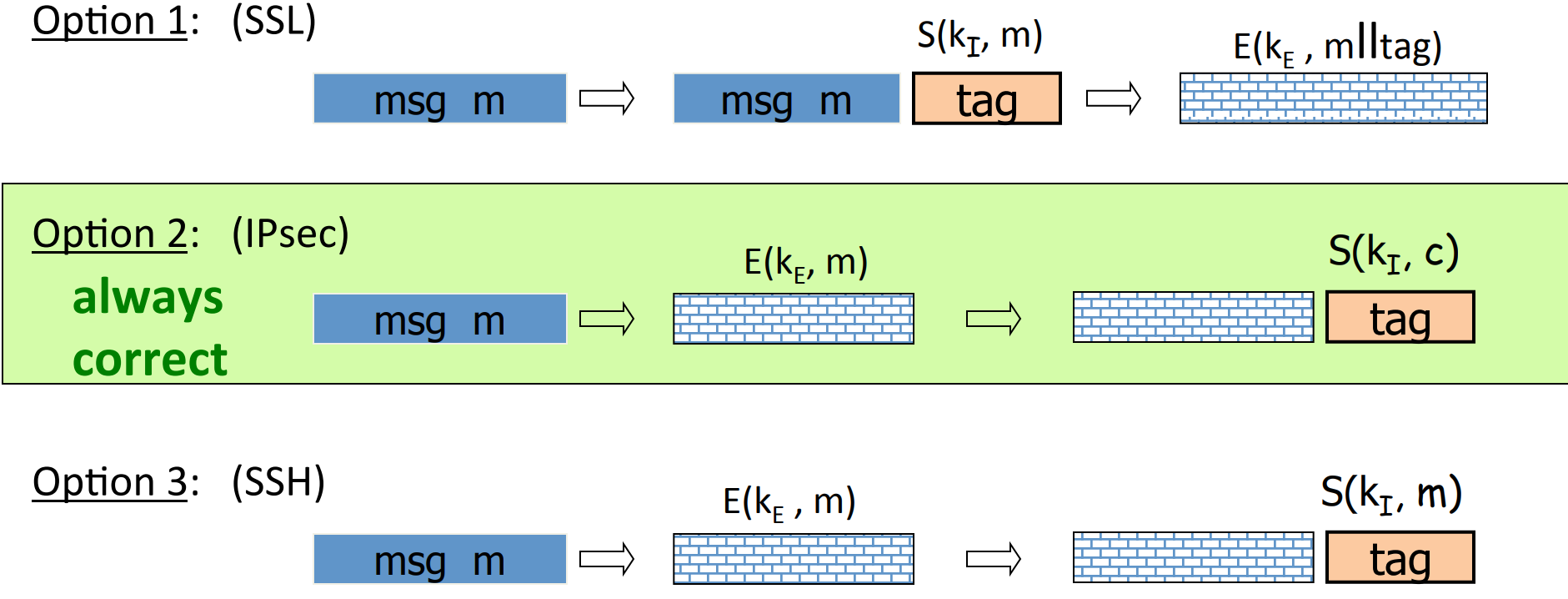
It’s quite natural that since we need both CPA secure and integrity, can we just combine the CPA secure cipher and a secure MAC ? There are three choices:
MAC-then-encrypt (SSL), which means that tag forMACis also encrypted.- encrypt-then-
MAC(IPsec), which means that the tag is for the encrypted cipher text and not encrypted. - encrypt-and-
MAC(SSH), which means that the tag is for the plain text and not encrypted.
![57]()
AE theorems:
- encrypt-then-
MACalways providesAE. MAC-then-encrypt may be insecure againstCCAattacks. However when is rand-CTRmode or rand-CBCmode, then it providesAE.
Standards:
GCM:CTR-mode encryption then CW-MAC(Carter-WegmenMAC).CCM:CBC-MACthenCTR-mode encryption.EAX:CTR-mode encryption thenCMAC.
Instead of the combination of secure encryption and MAC , can we construct the AE mode directly? Yes, it’s OCB -mode:
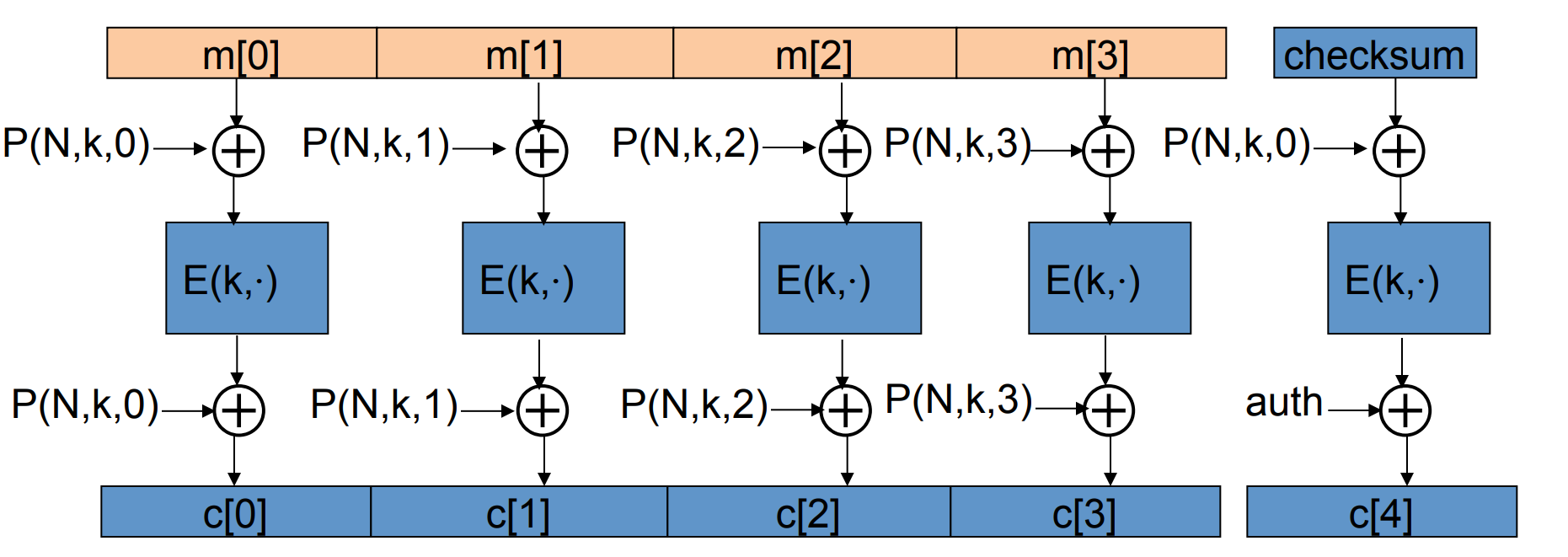
where is a secure PRP , and is similar to the one in PMAC , the purpose of it is to emphasize the order. And is nouce, which should be distince between messages but does not need to be random, so a counter is sufficient.
# CBC paddings attacks
Consider the MAC -then-encrypt mode, the decryption is three steps:
- Decrypt the cipher text.
- Check the padding to see if it’s valid.
- Check the tag to see the integrity.
So there are two petential erros: Padding error and MAC error.
Suppose the attacker can distinguish the two types of erros, then he can submit ciphertext and learns if last bytes of plaintext are a valid pad.
Let’s give an example for CBC encryption:
If we want to know the very last byte of the plaintext, then we just iterate , and change the last byte of the second last block:
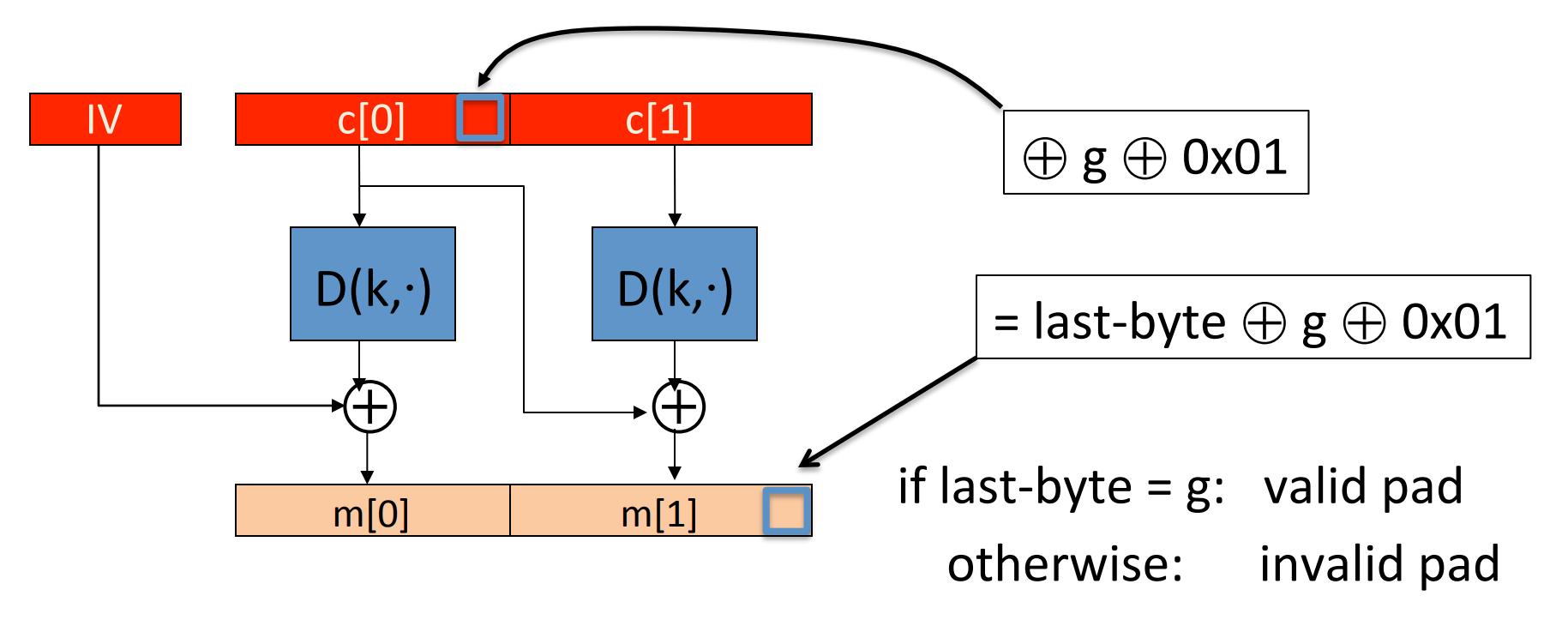
We know that is a valid pad. So if and only if when the last byte of the last block is equal to , then the decryption of it will be , and is a valid padding. Otherwise the attacker will get a padding error.
Similarly, by different length of padding, the attacker can get the bytes one by one.
However, encrypt-then- MAC will completely avoid this problem.
# Special attack: attack on non-atomic decryption
Example: SSH Binary Packet Protocol
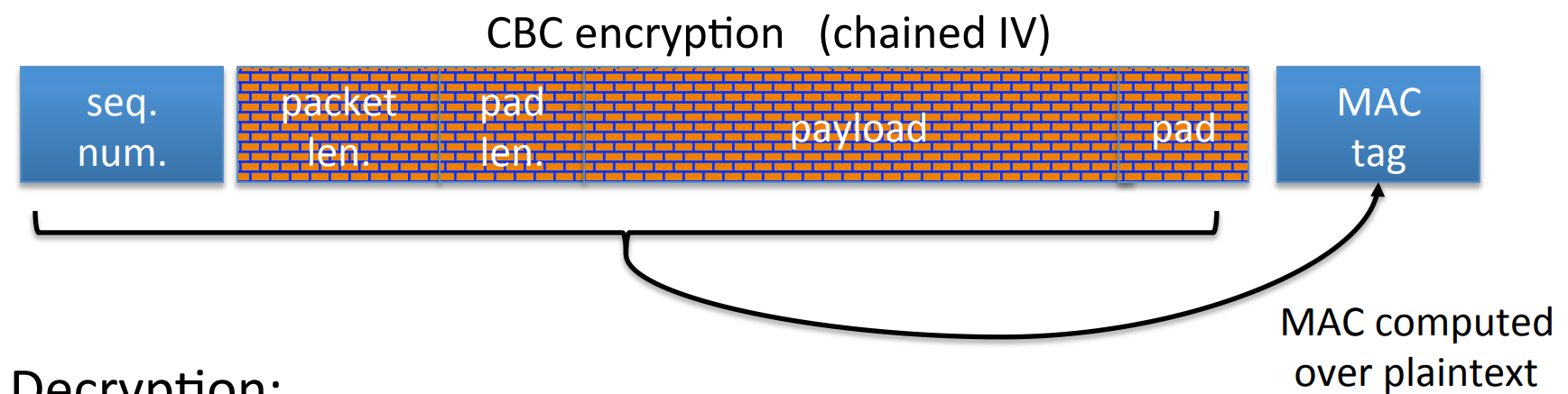
The process of decryption is:
- decrypt packet length field only!
- read as many packets as length specifies.
- decrypt remaining ciphertext blocks.
- chech the
MACtag.
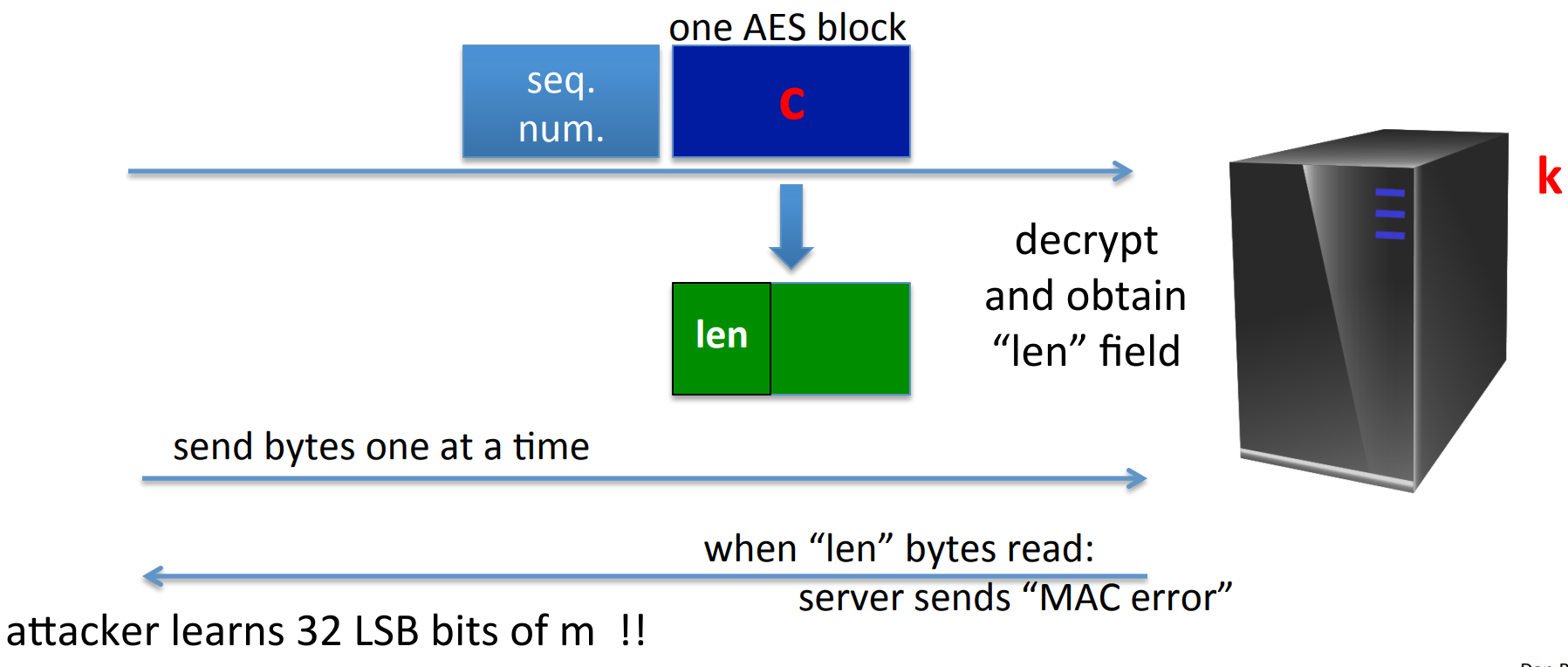
So if the attacker wants to know the plaintext of a given ciphertext (Notice here the ciphertext is given but not constructed by attacker, so it’s not a CCA attack), then it can repeat sending 1-byte messages to the server until get a “ MAC -error”, then the left 32 bits of the plaintext (length field) will be learned by the attacker.
# Odds and ends
# Key derivation
Suppose the source key SK is uniform in , and is a PRF with key space and outputs in .
And we can construct a Key Derivation Function KDF as:
where is used to identify different applications, even two applications have the same SK , they will get the different key.
What will happen if the SK is not uniform?
We know that the PRF 's outputs will not look like random any more.
The solution is Extract-then-Expand paradigm:
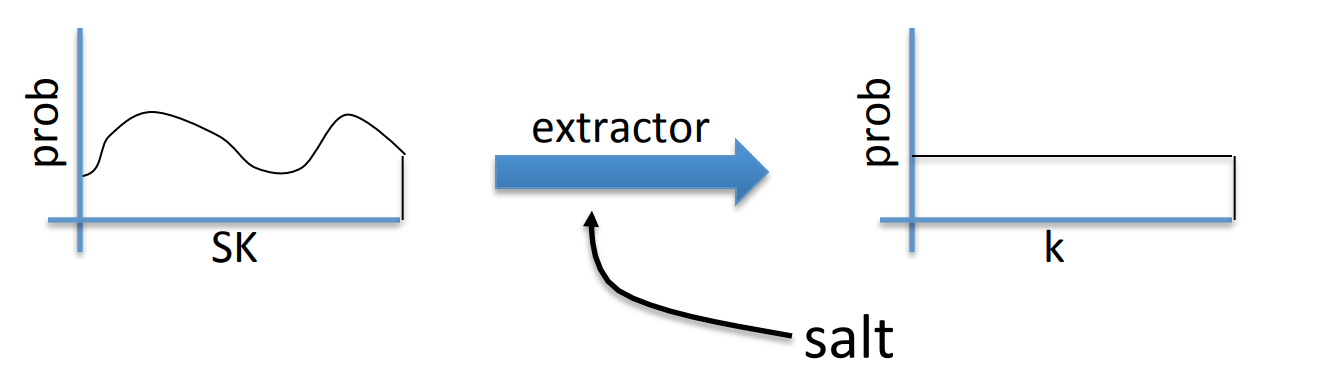
where salt is a fixed non-secret string chosen at random, and after the extraction, the distribution will be uniform.
The implemention of the extractor is not going to be discussed here, but we know that HKDF is a KDF based on HMAC , which is widely used.
Another KDF is Password-Based Key Derivation Function PBKDF .
Since the passwords have insufficient entropy and are vunerable to the dictionary attack.
So we need a new paradigm: Password-Based Key Derivation Function, it improves salt and slow hash function. The standard approach is PKCS#5 , iterate hash function times.
# Deterministic encryption
The deterministic encryption is for the cases when there is nounce or other random stuff, so if the key and the plaintext is fixed, the ciphertext is also fixed.
One example is the server querying the database. Each data entry has a “index” (Alice, Bob,…) and is encrypted in the database. When the server want to query, it sends the encrypted index, and database compares the encrypted index and sends back the encrypted data. The database doesn’t learn anything about plaintext in the whole process.
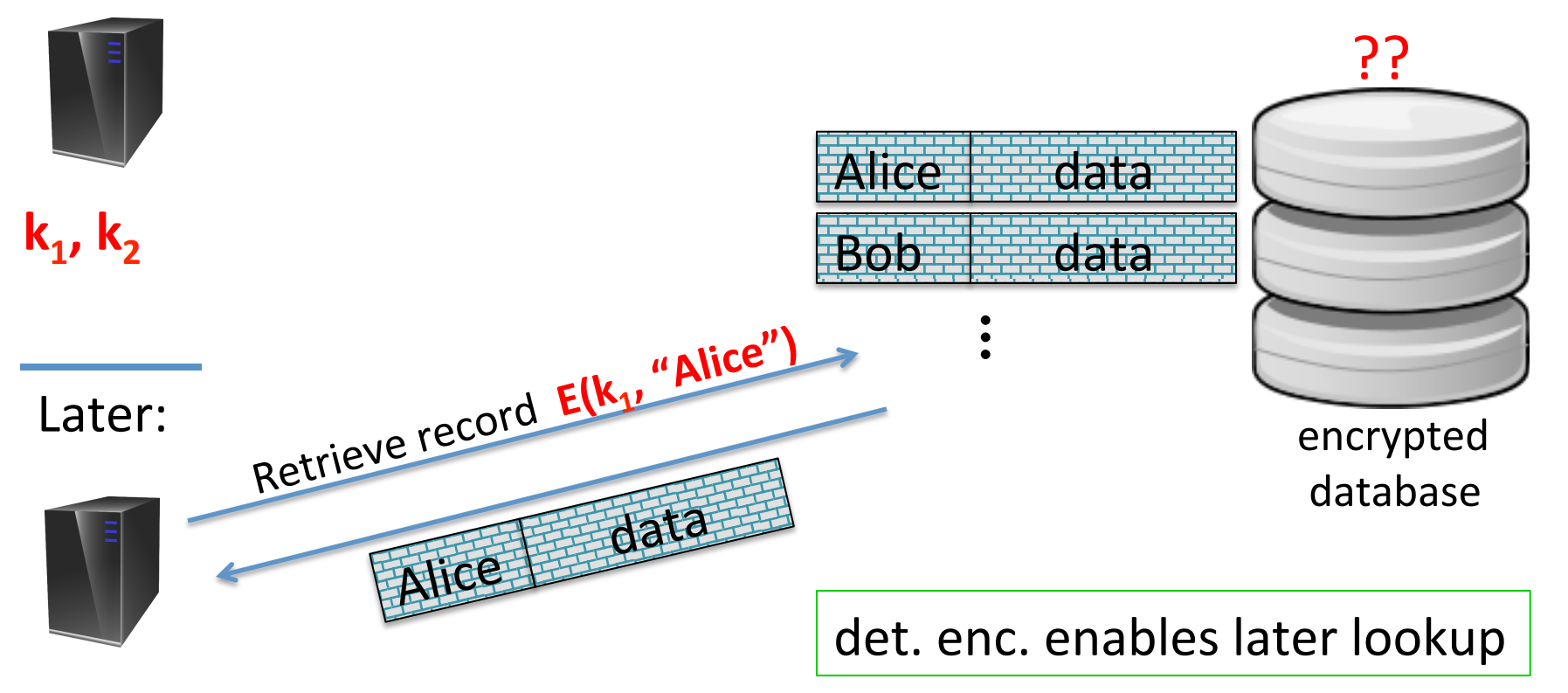
However, determinism means that two same messages are encrypted into same ciphertext, which leaks information. It cannot be CPA secure:
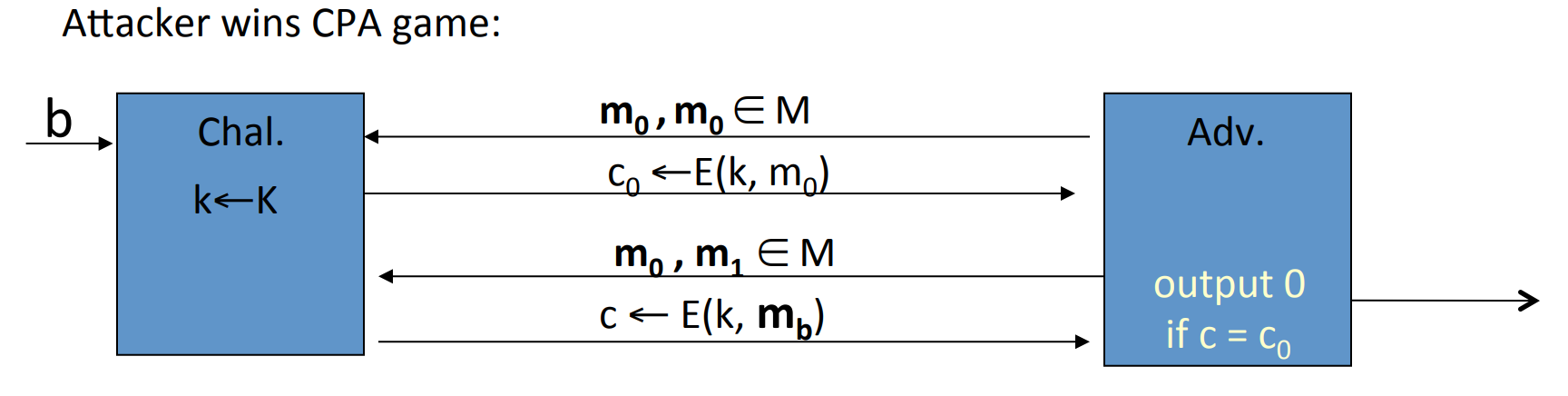
The solution is quite simple, the message structure can be unique like UserID.
So in this case, we can define Deterministic CPA secure:

if for all efficient ,
is neglibigle.
The most different here is that and should all be distinct. Let’s see some examples:
- Example:
CBCwith fixedIVis not deterministicCPAsecure:
![66]()
- Example:
CTR-mode with fixedIVis not deterministicCPAsecure:
![67]()
# Deterministic encryption constructions: SIV and wide PRP
Construction 1. Synthtic IV ( SIV )
Let be a CPA -secure encryption and be a secure PRF . Then we define:
Since is indistinguishable from a real random choice, is semantically secure under determinstic CPA .
In the previous discussion we know that confidentiality cannot be guaranteed without integrity, so we need to achieve Deterministic authenticated encryption ( DAE ).
Consider a SIV special case, SIV-CTR :
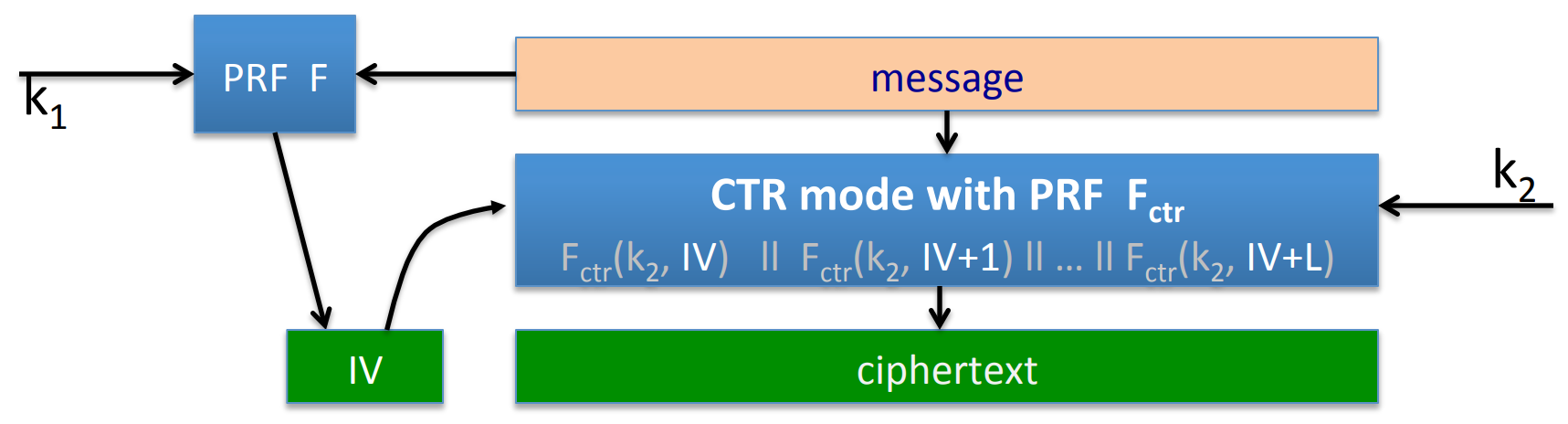
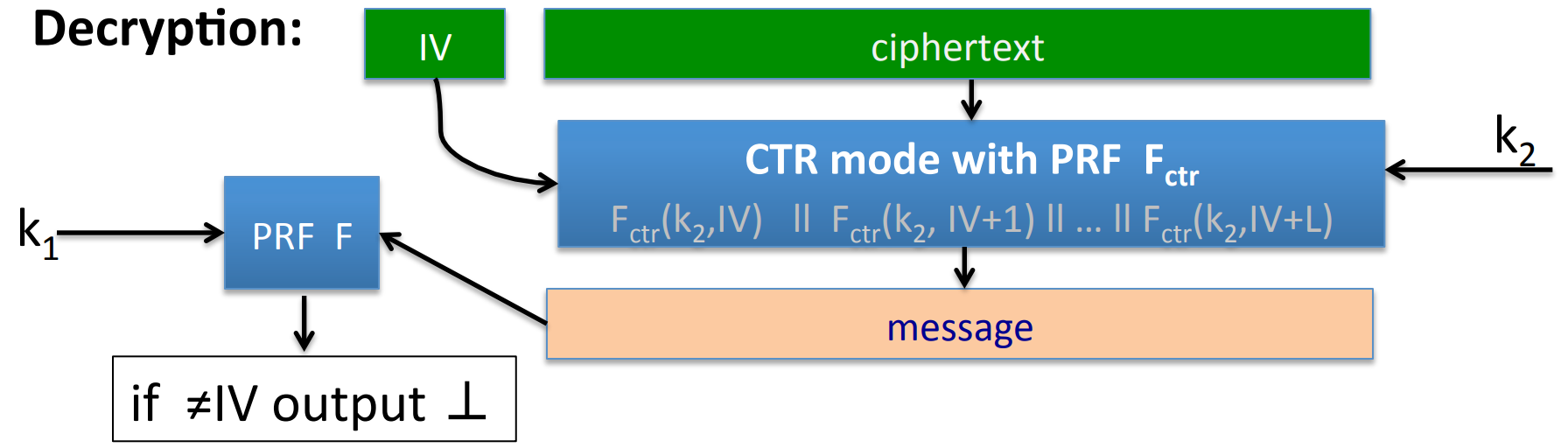
Theorem: if is a secure PRF and from CTR -mode is CPA secure, then SIV-CTR provides DAE .
Construction 2. just use a PRP
Let be a secure PRP , , then it is semantically secure under deterministic CPA .
In the game, the adversary would only see q different random values in so he cannot learn anything about plaintext.
However, construction of PRP in a large message space is not easy. And we will introduce EME to construct a wide block PRP .
Goal: let be a secure PRP , we can construct a PRP on where :
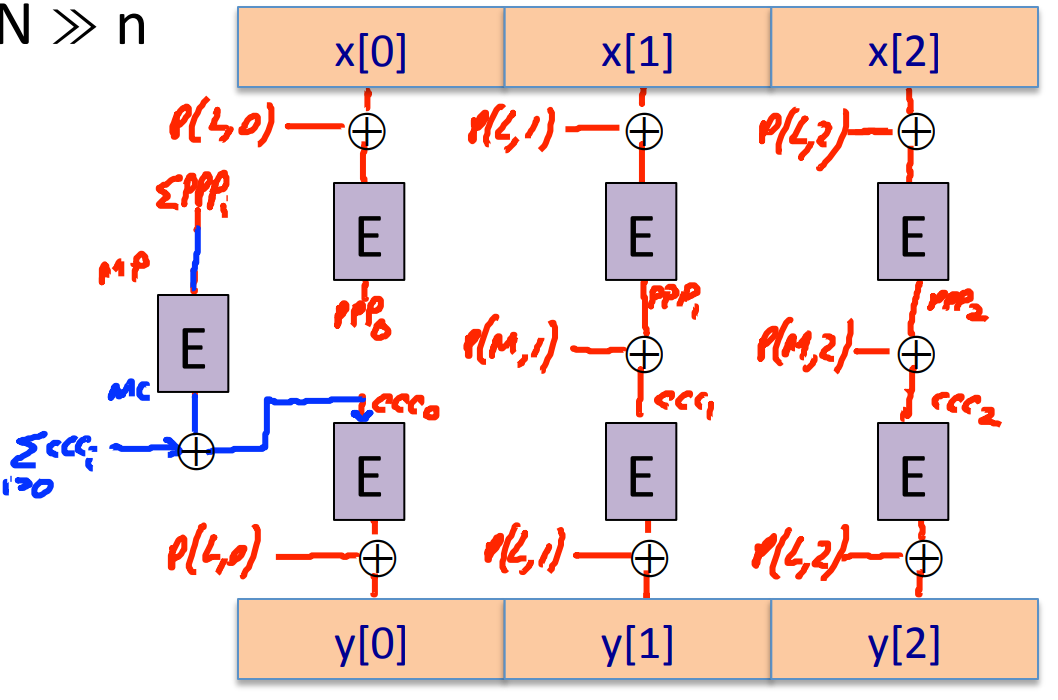
where , , , and function is similar in the previous construction.
Each function is .
PRP -based deterministic CPA secure is quite simple, if is a secure PRP , then:
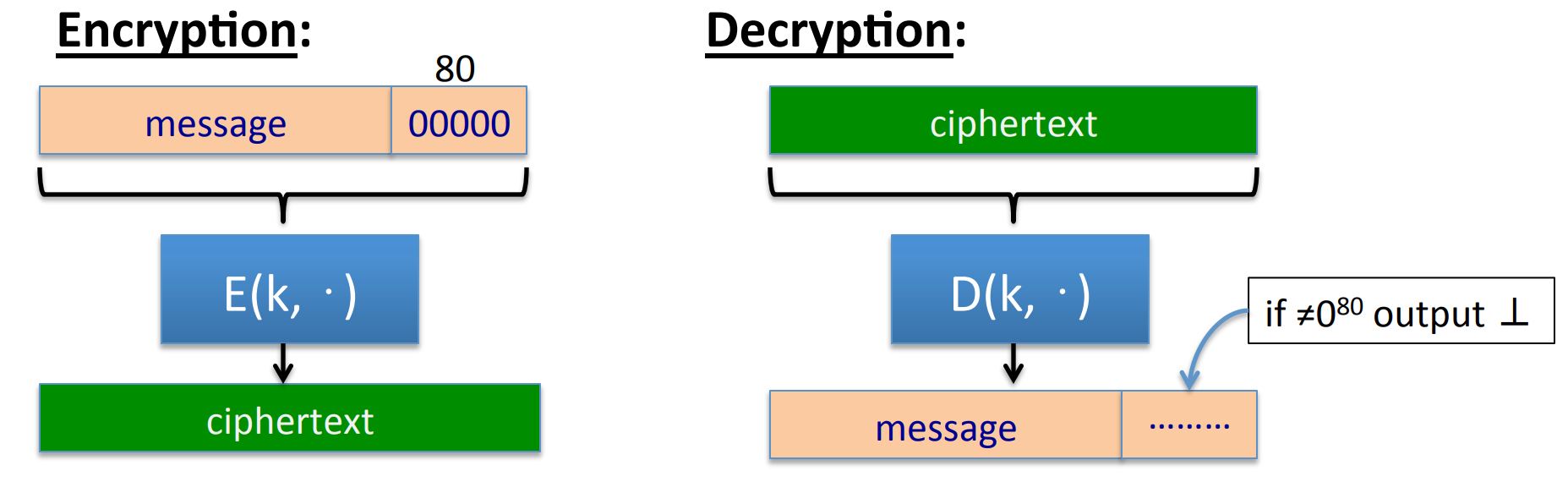
provides DAE .
# Tweakable encryption
An example that we need tweakable encryption is the disk encryption. Since the disk space is fixed, we need the ciphertext to have no expansion.
If we use PRP to encrypt:
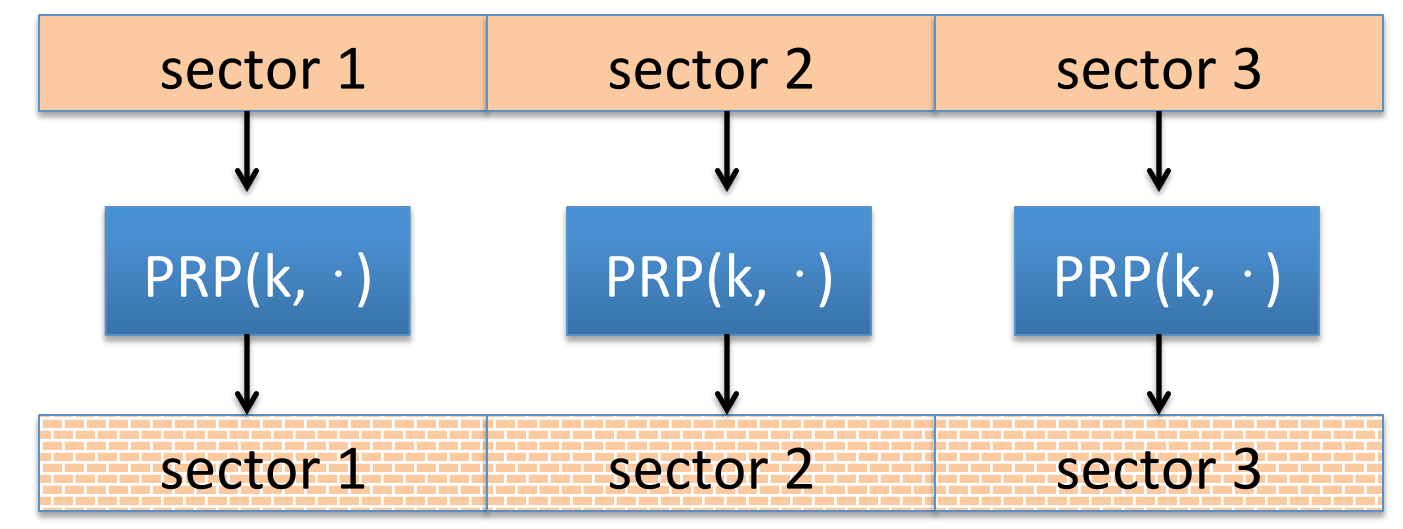
then sector 1 and sector 3 may have the same context. So we improve:
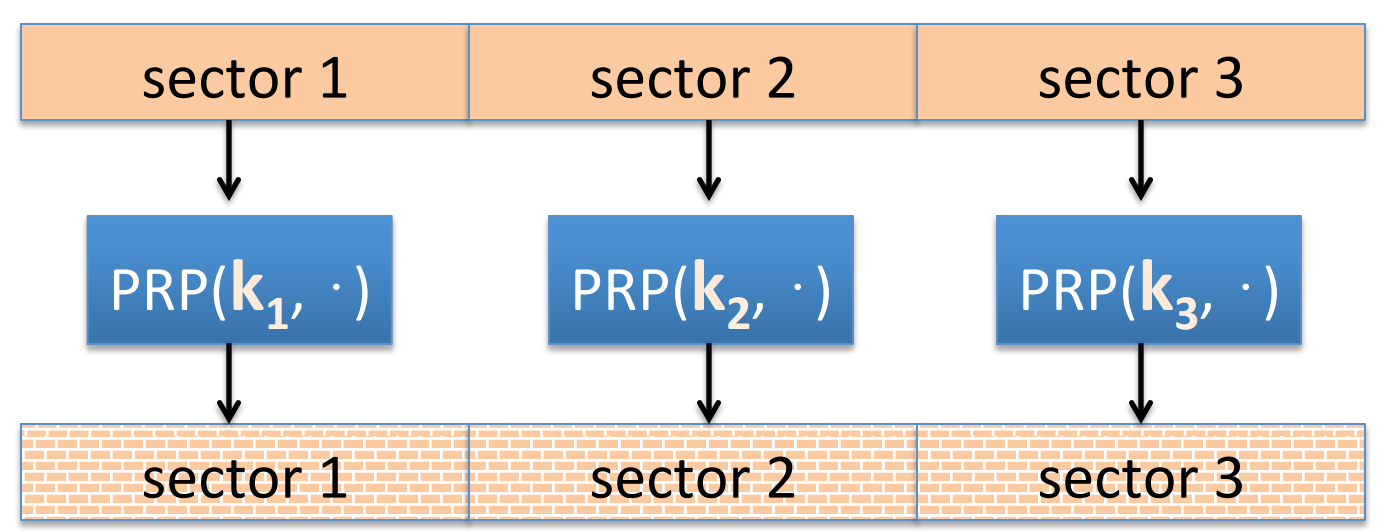
in this case, the attacker can tell if a block is changed and then revert.
But the problem is quite troublesome to solve, so we just ignore it here.
Obviously in the construction we need to manage several keys.
Goal: construct many PRP s from a key.
, where is called tweak. We use the number of sectors as the tweak. We hope that is indistinguishable from a random permutation on .
And we can define a secure block ciphers:

The trivial construction:
let be a secure PRP , and:
XTS tweakable block cipher:
let be a secure PRP , and:

and function are used to distinguish index and order,
Summary:
- Use tweakable encryption when you need many independent
PRPs from one key. - XTS is more efficient than the trivial construction, but both are narrow blocks.
EMEis a tweakable mode for wide blocks, but slower.
# Format preserving encryption
For example, the card number may have some fixed format: bbbb bbnn nnnn nnnc.
And the encrypted card should “look like” a credit card, so we need Format Preserving Encryption ( FPE ).
Suppose is the total # credit cards in the world. Then the encryption process is:
- map given card number to .
- apply
PRPand get an output in . - map out back to a card number.
Given a secure PRF , we can construct such PRP .
Step 1.: from to where . Here we can use the Luby-Rackoff with truncate :
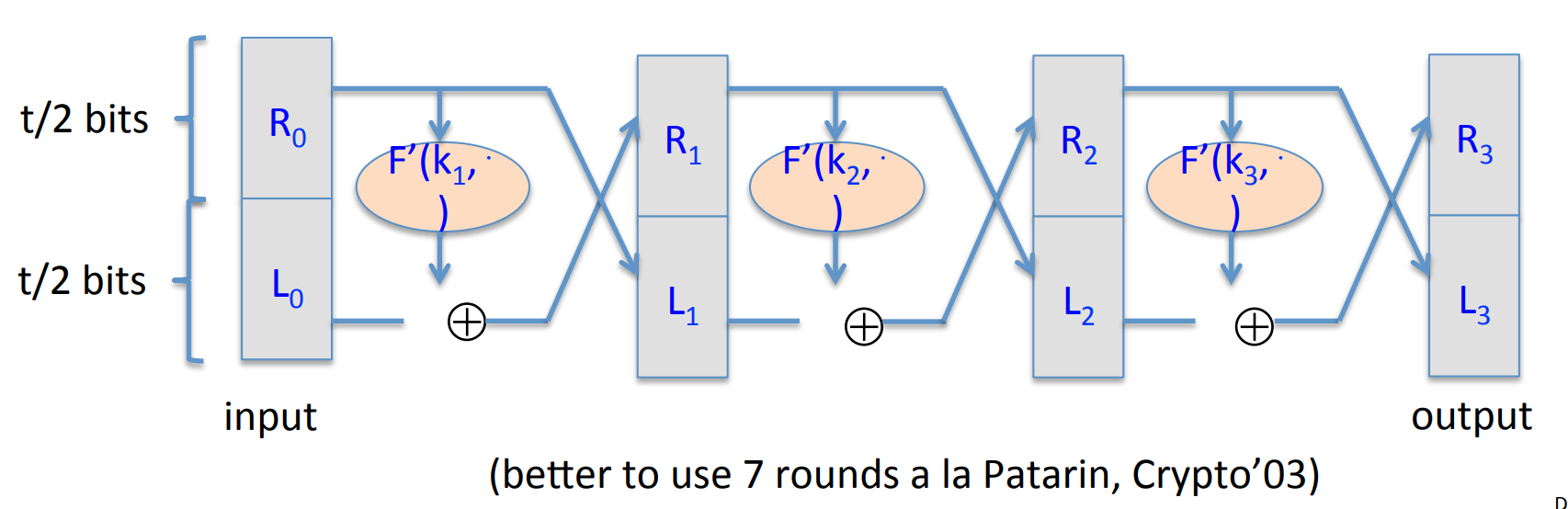
Step 2.: from to . Since is a subset of , the construction of is quite simple: iterate until the output is inside the subset:

since , so it will not take too long to find the output.
Noticing: FPE guarantees no integrity.
# Basic Key exchange
# Trusted party
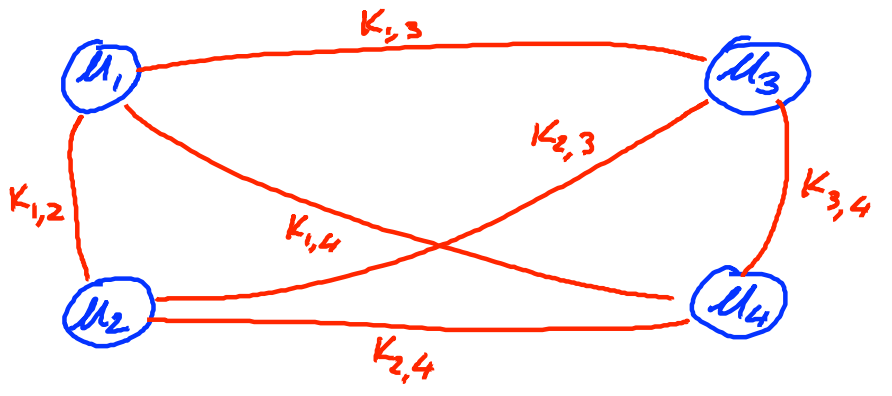
Problem: When a bunch of users need to communicate with each other, then for a user he may need to store several distinct keys for different opponents:
A better solution is to make an online Trusted 3rd party ( TTP ):
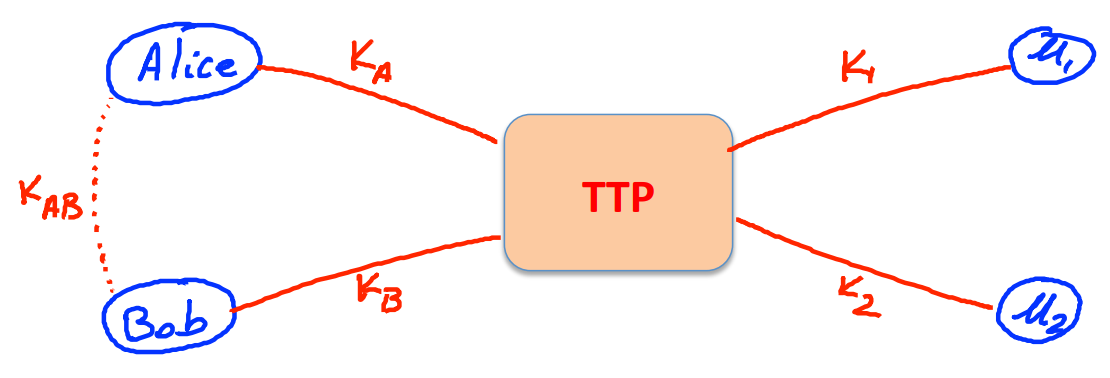
So that each user just needs to store one key with TTP .
A toy protocol: If Alice wants a shared secret key with Bob, then she asked the TTP , then TTP returns two messages:
the first message is for Alice who has , so she could decrypt and learn . The second message will be sent to Alice, but Alice will send it to Bob who has , so Bob will also learn .
If is CPA -secure, then the eavedropper will learn nothing about .
However the protocol is insecure against replay attack since the attacker can record the session between Alice and Bob, then replay it. So Bob may be fooled that Alice ordered the commodity twice.
Problem: Can we generate shared keys without TTP ? -Yes!
- Merkle(1974)
- Diffie-Hellman(1976)
- RSA(1977)
# Merkle puzzles
Goal: Just by the communication between Alice and Bob, to generate a shared key safely.
Here is an easy but inefficient method: Merkle puzzles.
Here are what Alice and Bob should do:
- Alice: prepare puzzles,
- For choose a random and , set:
- Then send the puzzles to Bob.
- Bob: Choose a random , and solve it, obtain , then send back to Alice.
- Alice: receive , then get the shared key .
For Alice, she needs to construct puzzles, so the work is (If we think function and random function is )
For Bob, he needs to solve a puzzle. The method is just to try every , so it also takes time .
But for an eavedropper, Although he can break the puzzle and get , but he does not know which is , he needs to break all puzzles to find . So the work is .
The different effort needed for Alice, Bob and eavedropper is the key reason that the method is secure. However, it’s not that efficient.
# The Diffie-Hellman protocol
Goal: Just by the communication between Alice and Bob, to generate a shared key safely.
Protocol:
- Fix a large prime number (e.g. 600 digits).
- Fix an integer .
- Alice: Choose a random , send to Bob.
- Bob: Choose a random , send to Alice.
- Then the shared key is .
For Alice, she can computer the key by , and for Bob he can compute by .
However, for eavedropper who just knows , it’s quite difficult to computer . The function is much slower than function. The run time may be (GNFS algorithm, best known). If the operator is defined on elliptic curve group, then it takes more time to compute , roughly .
However, the protocol is insecure to Man-in-the-Middle MiTM attack:
- Alice sends to
MiTM. MiTMfalsifies a , and sends to Bob.- Bob sends to
MiTM. MiTMfalsifies a , and sends to Alice.
So now, Alice thinks that the shared key is , and Bob thinks that the shared key is .
But the eavedropper knows , so he can compute .
An open problem: If several users what to communicate with each other, they all have a and share on cloude or facebook, then can one generate a shared key with other users?
when the key is only shared by two users, we use DH protocol, but when the key is shared by four more users, the problem is not solved yet.
# Public-key encryption
Definition: a public-key encryption system is a triple of algorithms :
- outputs a random key pair .
- encrypts a message with public key .
- decrypts a ciphertext with secret key .
Consistency: .
The semantic secure of public-key encryption:

is semantic secure (a.k.a IND-CPA) if for all efficient ,
is negligigle.
Then we can establish a shared key:
- Alice: use to generate , and send "Alice, " to Bob.
- Bob: Choose a random , and send “Bob,” to Alice.
- Alice: receive “Bob,”, then compute . is the shared key.
The adversary can only obtain , and cannot learn about , since it’s indistinguishable from a real random number.
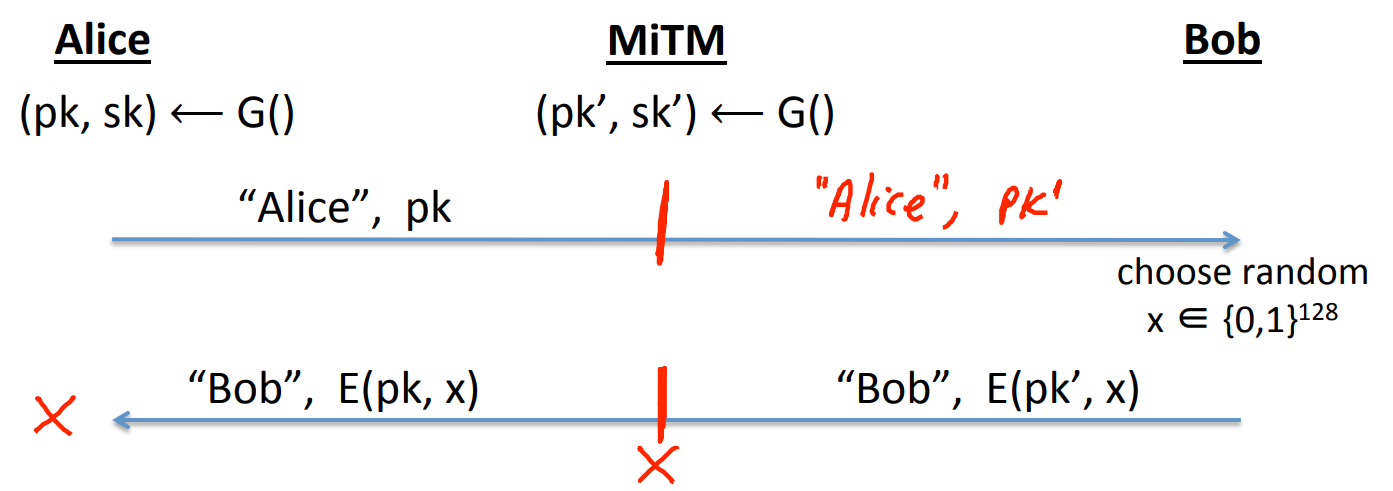
However, the encryption is still insecure against MiTM attack:
# Basic number theory
Lemma: has an inverse if and only if .
Proof: , then exists s.t. , then .
If , then . If , then exists , such that , then , so .
We define .
Fermat’s Theorem: let be a prime, then .
In contrast, if , then .
Definition: For , the set is called the group generated by , denoted as .
The order of is the smallest s.t. , denoted as , also is the size of .
Lagrange Theorem: , divides .
Euler Theorem: let , then , .
Definition: let be an odd prime, is a quadratic residue ( QR ) if it has a square root, that is, .
Theorem: is a QR in , And is called the Legendre symbol of over . Then .
# Intractible problems
is a very complexed function.
So a CR hash function is defined as .
To find a collision for : , then we need to compute , we need to use function, which is quite hard.
Let , then the problems are intractible:
- Factor a random in .
- Given a polynomial and a random , to find a s.t. .
# Public Key Encryption from Trapdoor Permutations
# definitions and security
For symmetric ciphers we had two security notions:
- One-time security.
- Many-time security(
CPA).
and we showed that One-time security $\not\Rightarrow $ Many-time security, whichs means that a key should never be used more than once for one-time security.
However, for public key encryption, we need to guarantee that One-time security Many-time security. Since the attacker can always use the public key to encrypt any message at his will. And we hope the public key encryption must seem like randomized.
The definition of (pub-key)Chosen Ciphertext Security is a bit different:
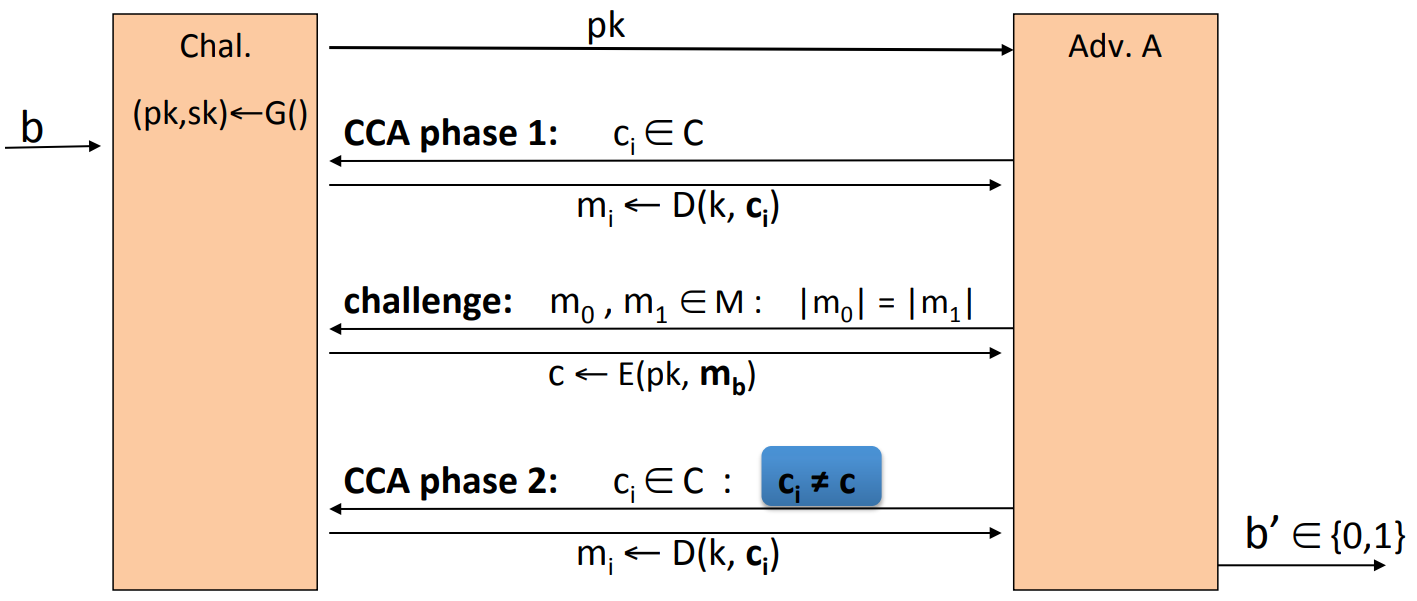
The difference is because a secure symmetric cipher must provide both security and integrity, roughly speaking to make sure that the attacker cannot construct ciphertext himself. However, for public key encryption, the attacker can always construct ciphertext himself, so we define and require the CCA secure directly.
Then is CCA secure (a.k.a IND-CCA) if for all efficient :
is negligible.
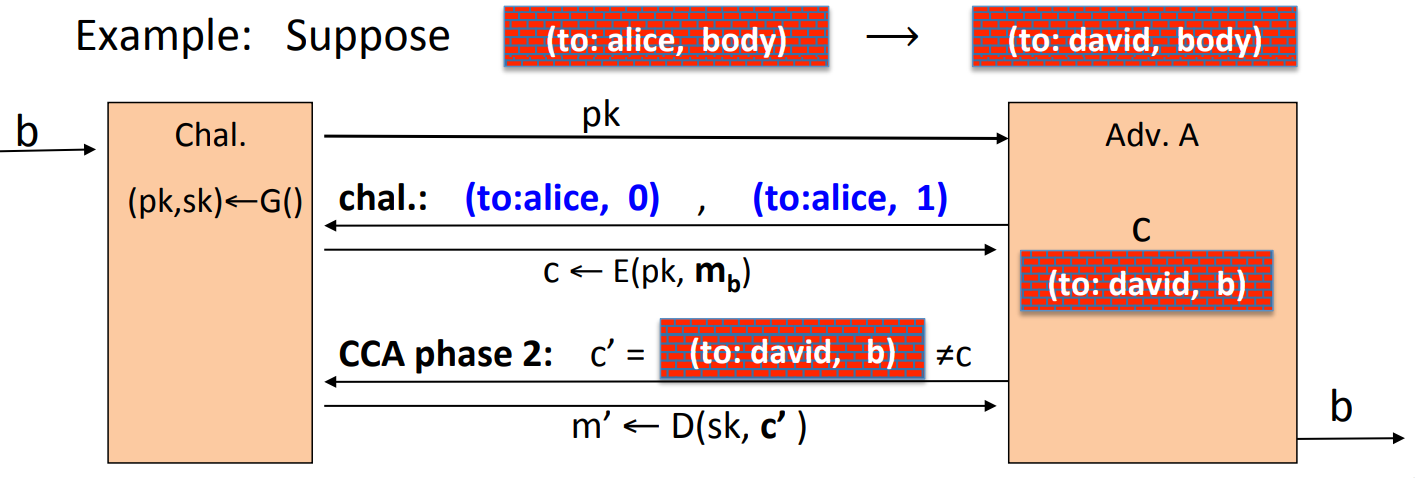
- Example, suppose an attacker has the ability to change the header of cipher text, and the corresponding plaintext is changed from “to: alice” to “to: david”, then the public key encryption is not secure:
![83]()
The attacker query for the ciphertext for “(to:alice,0)” and “(to:alice,1)”, and modify the ciphertext for “(to:alice,b)” to “(to:david,b)”, and then send back the ciphertext.
# Constructions
Definition: A trapdoor function ( TDF ) is a triple of efficient algorithms :
- is a randomized algorithm outputing a key pair .
- is a determined function .
- defines a function that inverts .
More precisely, .
Also, we define what is a secure trapdoor function:

To make sure that is a “one-way” function, which means it can be evaluated easily and cannot be inverted without .
We can construct public-key encryption from TDF :
- is a secure
TDF. - is a symmetric authentication secure encryption.
- is a hash function.
We construct:
Theorem: If is a secure TDF , provides authentication security, and is collision resistant, then is secure.
Remark: the little “ro” indicates that the security is set in a random oracle model, but not important here.
Never encrypt by applying directly to plaintext!
since it’s now deterministic and cannot be semantic secure, and has many attacks.
# The RSA trapdoor permutation
The RSA trapdoor permutation is first published on Scientific American in 1977, and is widely used in SSL/TLS, secure e-mail, secure file systems…
The RSA trapdoor permutation is:
- : choose two random primes 1024 bits, set . Choose integer s.t. . Output .
- .
- .
Consistency:
The RSA is a one-way function is based on the assumption that given , it’s hard to find .
Emphasize again: The RSA permutation is not an encryption scheme, so you never use it directly to encrypt messages.
Textbook RSA which is insecure:
- public key , encrypt: in .
- secret key , decrypt: in .
An simple attack is that, given a 64-bits , there probability that where . Then we have , so a man-in-the-middle attack will work. The total attack time is around .
# PKCS 1
PKCS1 v1.5
In practice we often apply some preprocessing to the plaintext before encryption, and the most common one is called PKCS 1 .
For example, if we need to setup a session and transmit a shared key, then the message may be a 128 bits AES key, we would append it:

where the first 2 bits are used to indentify it’s PKCS 1 mode 2 widely used in HTTPS, and the random pad should not contain ‘FF’, the resulting 2048 bits is sent to RSA encryption.
A simple attack to PKCS1 is discovered by Bleichenbacher, since the server always check the first two 2 bits are ‘02’ and return different error message, so we can:
- given a ciphertext and public key , send to server to check if the plaintext most significant bit is ‘02’.
- multiple the ciphertext by , then the plaintext is shifted by 2 bits, send to the server and we learn the next 2 bits:
- repeat the above process until we get the plaintext.
Attacks discovered by Bleichenbacher and Klima et al. can be
avoided by treating incorrectly formatted messages blocks in a manner indistinguishable from correctly formatted RSA blocks.
PKCS1 v2.0: OAEP
the message is padded with ‘01’ following several 0s, and followed by a randomized padding, are two collision resistant hash function (like random oracle):
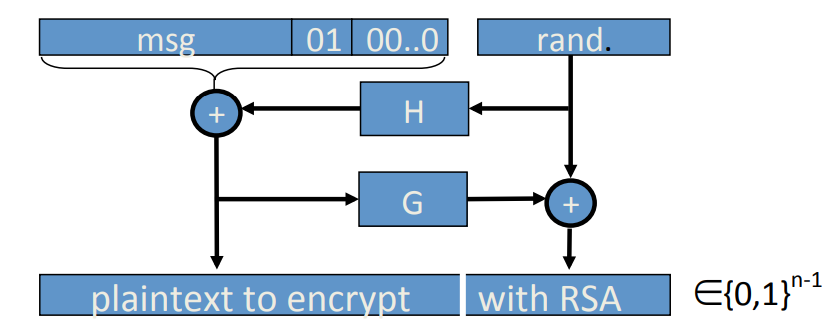
Theorem[FOPS’01] indicates that if are random oracles then RSA-OAEP is CCA secure. In practice we use SHA-256 for the hash functions.
Also there is OAEP+[Shoup’01] if we substitute the ‘0100…0’ by which is a random oracle:
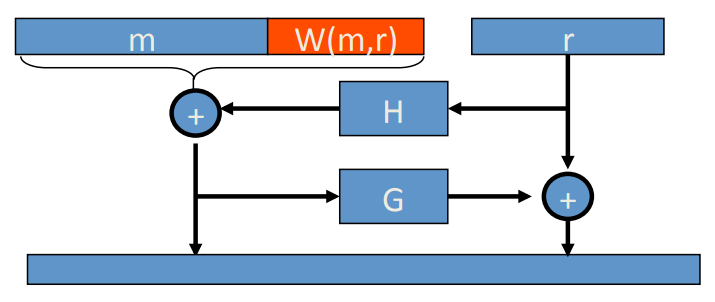
for any trapdoor permutation , F-OAEP+ is CCA secure if are all random oracles.
There is SAEP+[B’01]:
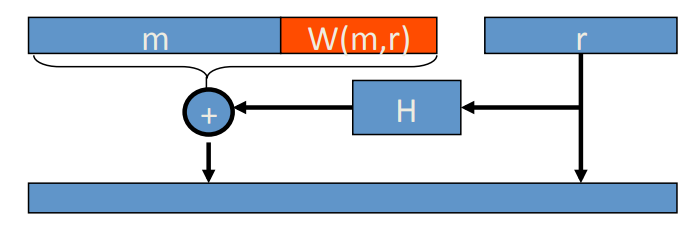
If RSA is a trapdoor permutation () then RSA-SAEP+ is CCA secure if are all random oracles.
What is notice worthy is that OAEP may be vulnerable to timing attack if is implemented incorrectly, so never implement it yourself.
# Is RSA a one-way function?
[Wiener’87] if then RSA is insecure.
Wiener’s attack:
since , then we have:
Since , then , and ,we have:
the inequality here is quite loose. Then since , So we have:
Remember that , so we have
Because , so . So:
The two rationals are so close here, so we can just try to find . And since , so , so somehow find and .
# RSA in practice
The recommended value for is , then choose randomly, compute . There are many potential attacks:
- Timing attack[Kocher et al. 1997]: the time to compute can expose .
- Power attack[Kocher at al. 1999]: The power consumption of a smartcard to compute can expose .
- Faults attack[BDL’97]: A computer error during can expose .
Faults attack example:
A common implementation of RSA is to compute and seprarately, then use 中国剩余定理 (Chinese Remainder Theorem, CRT ) to combine them to compute . (Obviously we have and )
So when is computed incorrectly, the result is , so we have:
So:
which reveals .
Besides, If two Internet applications use the same but different , we can also use to find . The experiment result is that about of public HTTPS keys can be factored!.
# Public key encryption from Diffie-Hellman: ElGamal
ElGamal: Converting Diffie-Hellman protocol to publick key encryption:
- : choose a random generator , and random , output .
- is a hash function.
Since is fixed before encryption, so we can pre-compute to speed up the computation of .
# ElGamal security
-
Computational DH assumption is for all efficient algorithm , is negligible. In other words, it is hard to compute by .
-
Hash DH assumption is:
where is a random generator in , are random elements in , is a random element in . We need the hash function to be indistinguishable from real random.*
Here acts as an extractor, is not uniform on but is a uniform distribution on .
Since the hash function is indistinguishable from real random, the semantic security for Hash DH assumption ElGamal is quite easy:
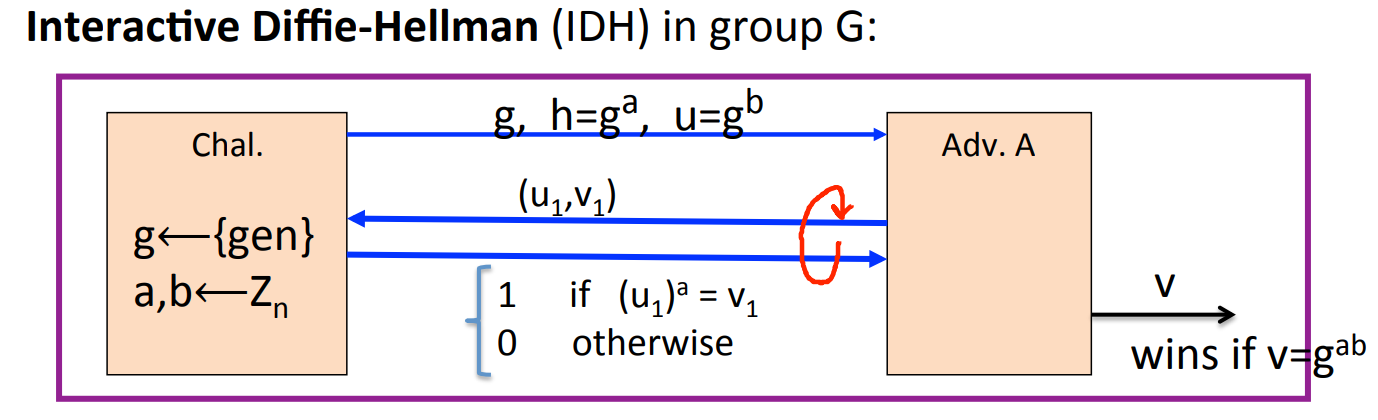
- Interactive HD assumption. To prove
CCAsecurity, we need stronger assumption-IDH. The game is:
![91]()
IDHholds if for any efficient and several queries, is negligible.
Theorem: If IDH holds in group , provides authentication security and is a random oracle, then ElGamal is secure.
# ElGamal variants with better security
Can we achieve CCA security just with CDH instead of IDH ? --Yes!
Twin ElGamal:
- : choose a random generator , and random , output .
Theorem: If CDH holds in group , provides authentication security, and is a random oracle, then twin ElGamal is secure.
Can we achieve CCA security without random oracle ? --Yes!
- Option 1. use
HDHassumption in “bilinear group” --special elliptic curve with more structure. [CHK’04+BB’04] - Option 2. use Decision-DH assumption in any group. [CS’98]
# A unifying theme
One-way function(informal): for all efficient , if is negligible for random in , then we think it as a one-way function.
Remark: why not just ask for ? Because the funtion extentionality, we think . e.g. is not a one-way function.
PRGis one-way function. Let be a securePRG, then it is a one-way function. Proof: if exists inverts , then we can construct to distinguishPRGfrom real random:
-
Discrete log is a one-way function. Computation of power is much eaiser than log, and is widely used in key-exchange and public-key encryption. .
-
RSAis a one-way function. is one-way function when , . It’s hard to calculate e-th root.