如果莎士比亚只会一个单词,那么他的皇皇巨著也就是在阿巴阿巴。
主要资料:
lec8.pdf (rutgers.edu)
Lecture 1 (mit.edu)
# introduction
Suppose we have a Boolean function , it defines a communication problem as follows: there are two players, say Alice and Bob, who get inputs and , respectively, and their goal is to compute .
For instance, in the equality problem, Alice and Bob would like to evaluate:
Considering neither Alice nor Bob has the entire input on their own, the players need to communicate with each other to determine the value of . The communication happens according to a protocol and is done as follows:
Alice sends a single bit to Bob based solely on her input; after receiving this bit, Bob responds back with a single bit of his own which is a function of his input and the message of Alice; the players continue this throughout the protocol; we assume that the last bit communicated by any player is the output of the problem.
The main measure of efficiency in this model is the communication cost of the protocols, defined as follows.
Definition(Communication cost). The communication cost of a protocol , denoted by , is the worst-case number of bits communicated between Alice and Bob in over any choice of inputs .
Definition(Deterministic communication complexity). The deterministic communication complexity of function is defined as , where ranges over all protocols that can solve .
Note that for any function as Alice can send all here -bit input to Bob, while Bob responding with 0’s between each one, and then Bob can output the final answer in another one bit.
# Protocol Trees
An easy way of describing a protocol between Alice and Bob is by using a protocol tree:
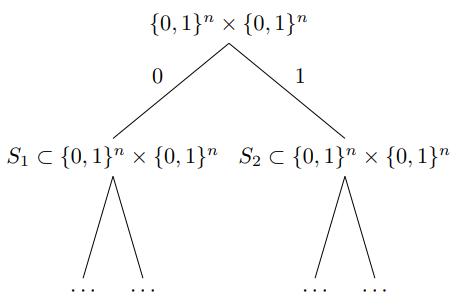
At the root of the tree, the left-child node contains all pairs such that Alice sends bit 0 for them and the right child-node contains the pairs where Alice sends 1 for them. We continue this way so that whenever we are at a node , the root-to-node path corresponds to the bits communicated so far.
Theorem(Rectangle Property). For a node in the protocol tree, the set assigned to it forms a combinatorial rectangle, i.e. for . In other word:
Proof:
Here is a video illustrating [Protocol Trees and Combinatorial Rectangles](Protocol Trees and Combinatorial Rectangles - YouTube) (strongly recommended). Let’s assume is a matrix representing function :
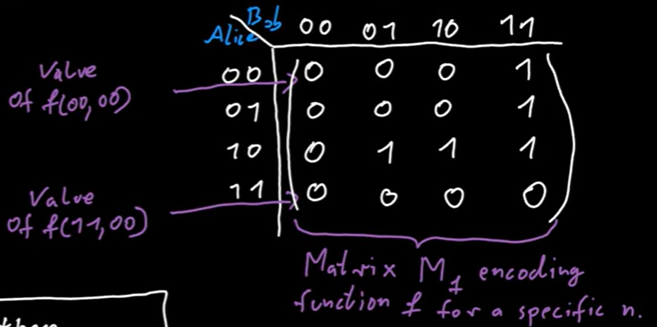
thus when Alice sends a bit, then some rows of the matrix is erased since the bit sent by Alice is only determined by the input for Alice and message already sent/received. The message is represented by the path from root to the node, which is fixed. So when we track the path from root to node , we are erasing some rows of matrix, some columns of matrix,… since we know the protocol and the message already sent.
For example, if we see Alice sends 0, then the input for Alice cannot be 00, so we erase a row of of matrix. Every path corresponds to a list of alternative removement, leading to a sub-matrix of all same elements (which is called monochromatic combinatorial rectangle, and “monochromatic” is for all same):
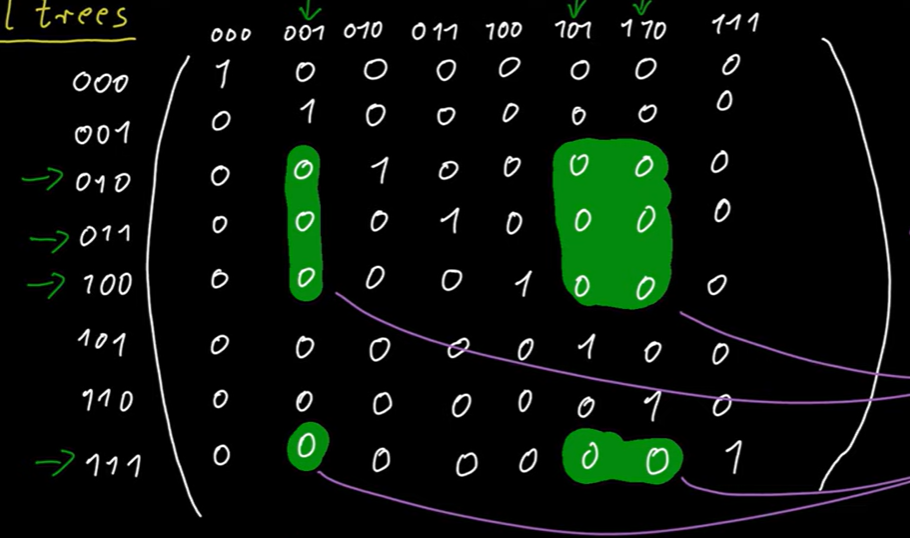
then we can compute the function . The theorem is saying that the left entries forms a sub-matrix, thus entries are left indicates are left.
.
Let denote the minimum monochromatic combinatorial rectangles needed to partition (the matrix representation for ).
Theorem: The number of leaves in a protocol tree is at least , thus the height of the tree is at least .
Example: For function ,
thus .
# A steaming lower bound for Distinct Element Problem
Theorem. Any deterministic streaming algorithm for computing DE exactly requires bits, given a stream of elements from the universe .
Proof: The proof comes from a reduction from Equality.
Consider an instance of EQ problem. Define the sub-streams:
where denote the -th/-th bits of . And let be the concatenation of two sub-streams.
An important property is that when , we have , while , either or .
Assume there is a deterministic streaming algorithm for computing DE that requires bits of space, now consider the following protocol for EQ based on . Alice generates and Bob generates locally, then Alice runs on , then sends the memory content and to Bob, which is bits.
Bob continues to run on with memory contents from Alice then get answer for . Thus Bob knows and can output by the property mentioned above.
Thus , which leads to .
.
# Randomized Communication Complexity
There are two ways of introducing random bits to the communication model
- the private coin/randomness model where Alice and Bob have access to separate sources of randomness on their own.
- the public coin/randomness model where players have access to a shared source of randomness.
Similar to other settings, we require that a randomized protocol for a problem to output the correct answer to for any given to Alice and Bob, with probability at least 2/3 (or some other constant strictly more than half).
Newman’s Theorem: Any public coin protocol for a communication problem with probability of success at least can be simulated by a private coin protocol such that and outputs the correct answer to with probability at least .
Proof:
Let denote the deterministic output of protocol on inputs and public randomness .
Lemma: For some , there exist strings such that for all , we have
Assuming the lemma, let’s see how to design a good protocol. Given the protocol , we can hardcode since they are independent of input . Then Alice samples an index and sends it to Bob, using bits, then Alice and Bob all simulates protocol with public random variable . It’s obvious to see that the protocol satisfies.
Proof of Lemma:
Define the indicator random variable for . By the guarantee of the protocol , we have that:
Now, suppose we sample public coins times. By Chernoff bound:
As such, by union bound over all choices of , we have,
If for all , we have "for all , ", then it must hold that
which contradicts. So there exists such .
.
Remark: Since we only care about communication complexity, thus we don’t care about how to find . We could assume that we have infinite local computing resources.
Remark: Newman’s theorem can be seen as a very basic pseudo-random number generator (PSG): We were able to reduce the entire random bits needed by to only bits (and thus communicate it between the players) at the cost of only paying an additive factor of in the algorithm. Note that aside from transforming public coins to private coins, this theorem also implies that any constant-error protocol can be made to work with only bits of randomness.
Definition(Communication cost). The communication cost of a randomized protocol is the worst-case number of bits communicated between Alice and Bob in over any choice of inputs and the randomness of the protocol.
We can view a public coin protocol as a distribution over deterministic protocols obtained by first using the public coins to sample the deterministic protocol and then running the deterministic protocol on the input. As such, we can alternatively define the communication cost of as the maximum communication cost of any deterministic protocol in the support of this distribution.
Definition(Randomized communication complexity). The randomized communication complexity of function is defined as , where ranges over all randomized protocols that can solve with probability of success at least 2/3.
Definition. Let be a distribution on inputs . We define the distributional communication complexity of over distribution as where ranges overall deterministic protocols that output the correct answer on inputs sampled from with probability at least 2/3.
Proposition(Yao’s minmax principle). For any communication problem :
- for all input distributions .
- for some input distribution .
Yao’s minimax principle gives us a way of proving lower bounds for randomized protocols by instead considering deterministic ones on random inputs (we typically only use the first part which follows from a simple averaging argument – the second part implies that this approach can always gives us the tightest possible bound if we are able to find the “right” distribution ).
# A example: Randomized Communication Complexity of Equality
Algorithm:
- Generate a public random string uniformly at random.
- Alice send to Bob.
- Bob also computes , and output .
Analysis:
when :
Thus when , with probability Bob outputs 1, and when , with probability Bob outputs 0.
The randomized communication complexity is since Alice just need to send 1 bit to Bob. And with Newman’s theorem, we can turn the above protocol into a private random protocol.
It is also worth mentioning that one can prove an bit lower bound on the communication cost of any private coin protocol for the equality problem. This in turn implies the tightness of Newman’s theorem (for constant ).
# One Way Communication Complexity: The Index Problem
Problem: In the index communication problem Ind , Alice gets a string and Bob gets an index ; the goal for the players is to output . i.e., .
Theorem. Any randomized streaming algorithm for computing DE exactly requires bits of space, where Ind is on domain .
Proof:
Assume there is a randomized streaming algorithm for computing DE that requires bits of space. Now consider an instance of Ind problem. Define the sub-streams:
and let be the concatenation of two sub-streams. An important property is, when , we have ; while we have .
Similar to the previous proof, we find a deduction from DE to Ind , in other way, we find a algorithm for Ind with space . Thus, .
.
Definition(One-way communication complexity). In the one-way communication model, we only allow Alice to send a single message to Bob and Bob then needs to output the answer.
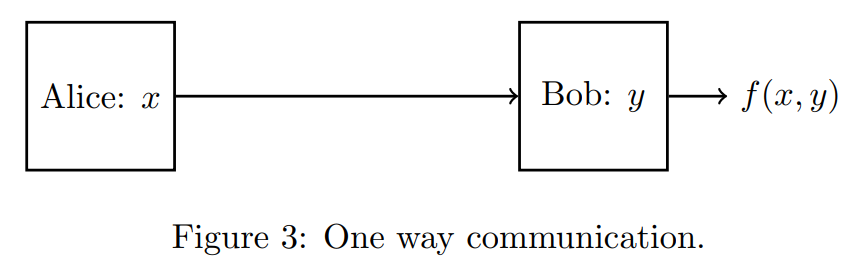
We then define
- One-way deterministic communication complexity: where ranges over all deterministic one-way protocols for .
- One-way randomized communication complexity: where ranges over all randomized one-way protocols for with probability of success at least .
- One-way distributional communication complexity: where ranges over all deterministic one-way protocols for with probability of success at least over the distribution .
is obvious, since by pigeonhole principle, if the message of Alice has size less than , then at least two different strings , are mapped to the same message . Now let be an index where . The output of Bob is a deterministic function of and and is thus wrong for one of and , a contradiction.
Theorem. .
Proof:
Let’s define the Hamming distance:
Lemma: For any parameter , there exists a subset with size such that for any two , .
Proof:
If are uniformly sampled from , we have:
By Chernoff bound,
Let and suppose we sample strings uniformly from . By union bound:
Thus there must exist satisfying the requirements.
.
The lemme illustrates a construction of “large” family of strings in that are “far from” each other.
We will use Yao’s minmax principle to show that there is a distribution where output the correct answer with probability 0.9 as opposed to 2/3.
With Lemma above, we can construct a set , for all for , and . In the distribution , we sample uniformly at random and give it to Alice, and sample uniformly at random and independently and give it to Bob.
Now consider any deterministic one-way protocol for Ind on the distribution with probability of success at least 0.9. By definition:
Let be the subset of :
We have as otherwise:
which contradicts.
For any , let denote the message sent by Alice to Bob when here input was (note that is a deterministic function of ). We claim that given only for any , we can recover the string entirely. The proof is as follows
Given , define the vector such that for any , i.e., the output of the protocol when the input to Alice is and input to Bob is . Note that is a deterministic function of only. Moreover we have
by the definition as only 0.2 fraction of entries of can be different from . On the other hand, for any , we have
As such, given , we can simply find the string which minimizes ; by the two equations above, this string has to be , thus allowing us to recover from . Since itself was a deterministic function of , we obtained a one-to-one mapping from for all . This implies that there needs to be , different messages sent by Alice, which means length of her message needs to be bits, concluding the proof.
.
# A reduction from nearest neighbor query to index problem
Problem(nearest neighbor search) NNS .
Given a stream of points in 2-dimensional Euclidean space and another point at the end of the stream. Assuming , to compute:
Intuitively, if we can solve this problem efficiently, then with same complexity can we determine that an element is in the set of not, which seems quite difficult.
Theorem. Any algorithm trying to solve NNS requires bits of storage.
Proof:
The proof is based on the reduction to Ind . Assuming there exists an algorithm computing NNS with bits. Now consider an instance for Ind problem , define points:
and sub-streams:
Let Alice run on and send storage to Bob, which needs bits. The answer of NNS on (whether ) doesn’t matter.
Then Bob continues to run on . If Bob outputs , which means there exists a point satisfying:
thus Bob could output 0 as the answer to Ind . Otherwise, he ought to output 1. Thus, we have .
.