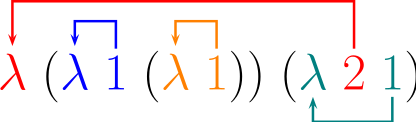幸福迟了一夜才来。

# 无类型系统

# 无类型算术表达式

# 语法

• 项的集合是最小集合$\mathcal{T}$，满足：
  • $\{true,false,0\}\subseteq \mathcal{T}$。
  • 如果$t_1\in\mathcal{T}$，则$\{succ\;t_1,pred\;t_1\;iszero\;t_1\}\subseteq \mathcal{T}$。
  • 如果$t_1,t_2,t_3\in\mathcal{T}$，则$if\;t_1\;then\;t_2\;else\;t_3\in\mathcal{T}$。

# 对项的一些归纳定义

常量集合：

$$Consts(true)=\{true\};Consts(false)=\{false\};Consts(0)=\{0\};\\ Consts(succ\;t_1)=Consts(t_1);Consts(pred\;t_1)=Consts(t_1);Consts(iszero\;t_1)=Consts(t_1);\\ Consts(if\;t_1\;then\;t_2\;else\;t_3)=Consts(t_1)\cup Consts(t_2)\cup Consts(t_3)$$

项的长度：

$$size(true)=size(false)=size(0)=1;\\ size(succ\;t_1)=size(pred\;t_1)=size(iszero\;t_1)=size(t_1)+1;\\ size(if\;t_1\;then\;t_2\;else\;t_3)=size(t_1)+size(t_2)+size(t_3)+1;$$

项的深度：

$$depth(true)=depth(false)=depth(0)=1;\\ depth(succ\;t_1)=depth(pred\;t_1)=depth(iszero\;t_1)=depth(t_1)+1;\\ depth(if\;t_1\;then\;t_2\;else\;t_3)=max(depth(t_1),depth(t_2),depth(t_3))+1;$$

有$|Consts(t)|\leq size(t)$。

同理，对项上的一个谓词，我们可以对长度或对深度归纳，或结构归纳。

# 求值

• 语法：

  $$t::=true|false|if\;t\;then\;t\;else\;t\\ v::=true|false$$

• 求值：

  $$if\;true\;then\;t_2\;else\;t_3\rightarrow t_2(E-IFTRUE)\\ if\;false\;then\;t_2\;else\;t_3\rightarrow t_3(E-IFFALSE)\\ \frac{t_1\rightarrow t_1'}{if\;t_1\;then\;t_2\;else\;t_3\rightarrow if\;t_1'\;then\;t_2\;else\;t_3}(E-IF)$$

  $t\rightarrow t'$ 表示 “t 一步求值为 t’”，意思是如果 t 是抽象机器在某瞬间的状态，则机器可以做一步计算，并将状态转换为 t’ .

# 无类型算术表达式

• 语法形式:

  $$t::=0|succ\;t|pred\;t|iszero\;t|true|false|if\;t\;then\;t\;else\;t\\ v::=nv|true|false\\ nv::=0|succ\;nv$$

  我们常用阿拉伯数字来记$succ\;0=1,succ\;succ\;0=2,...$

• 求值规则:

  $$if\;true\;then\;t_2\;else\;t_3\rightarrow t_2\quad(E-IFTRUE)\\ if\;false\;then\;t_2\;else\;t_3\rightarrow t_3\quad(E-IFFALSE)\\ \frac{t_1\rightarrow t_1'}{if\;t_1\;then\;t_2\;else\;t_3\rightarrow if\;t_1'\;then\;t_2\;else\;t_3}\quad(E-IF)\\ \frac{t_1\rightarrow t_1'}{succ\;t_1\rightarrow succ t_1'}\quad(E-SUCC)\\ pred\;0\rightarrow 0\quad(E-PREDZERO)\\ pred(succ\;nv_1)\rightarrow nv_1\quad(E-PREDSUCC)\\ \frac{t_1\rightarrow t_1'}{pred\;t_1\rightarrow pred\;t_1'}\quad(E-PRED)\\ iszero\;0\rightarrow true\quad(E-ISZEROZERO)\\ iszero(succ\;nv_1)\rightarrow false\quad(E-ISZEROSUCC)\\ \frac{t_1\rightarrow t_1'}{iszero\;t_1\rightarrow iszero\;t_2}\quad(E-ISZERO)$$

  项 t 被称为范式当且仅当不存在$t'$ 使得$t\rightarrow t'$.

  显然，范式就是那些$true,false,0,succ(0),succ(succ(0)),...$. 注意，若出现了 pred 一定不是范式，因为总可以用 E-PREDZERO 或 E-PREDSUCC 把它消掉.

  我们认为$succ\;true$ 是一个错误而不是一个值.

• 定义，如果一个封闭项是一个范式但不是一个值，则称该项受阻。

# 无类型的 lambda 演算

# 基础

• lambda 演算用最可能纯的形式表示函数的定义和应用。在 lambda 演算中，每个事物均是一个函数：函数接受的参数是函数，一个函数的结果是另一个函数。

• lambda 演算的语法由 3 种项组成。一个变量 x 本身是一个项；一个变量 x 在项$t_1$ 中的抽象，记为$\lambda x.t_1$，是一个项；并且一个项应用到另一个项$t_1\;t_2$ 也是一个项。用语法描述，项为：

  $$t::=x|\lambda x.t|t\;t$$

  我们规定，分析 lambda 演算式子时，从左到右分析，而抽象的顺序是从右到左。即：

  $$t_1\;t_2\;t_3=(t_1\;t_2)\;t_3\\ \lambda x.\lambda y.t=\lambda x.(\lambda y.t)$$

# 抽象语法和具体语法

# 辖域

• 对变量 x，当它出现在抽象$\lambda x.t$ 的 t 中时，则认为 x 的出现是囿界（或称被界定）的。等价地，也可以说$\lambda x$ 是一个绑定器，它的辖域是 t。x 是自由的如果它出现的位置不被任何对 x 的抽象所界定。比如 x 在$xy$ 和$\lambda y.xy$ 中式自由的，而在$(\lambda x.x)x$ 中的第一个出现是囿界的，而第二个是自由的。

• 一个不含自由变量的项称为封闭项（或称为组合子）。最简单的组合子就是恒等函数：

  $$id=\lambda x.x$$

• 规定，抽象总是尽量向右延展的，而应用是从左到右的。譬如：

  $$\lambda x.x\;y=\lambda x.(x\;y)\neq(\lambda x.x)y\\ (\lambda x.x\;y)a\rightarrow a\;y\\ (\lambda x.x)y\;a\rightarrow y\;a\\ idx\;y=(idx)\;y$$

# 操作语义

• 纯形式的 lambda 演算没有内置的常量或原语算子 —— 没有数、算术运算、条件子、记录、循环、序列、I/O 等到。项计算的唯一含义是将函数应用到参数（而参数本身也是函数）。

  计算的每一步是重写一个左端部分为抽象的应用，用右端部分代换抽象体中的囿变量。

  $$(\lambda x.t_{12})t_2\rightarrow [x\mapsto t_2]t_{12}$$

  其中$[x\mapsto t_2]t_{12}$ 表示由$t_2$ 代换在$t_{12}$ 中所有出现的 x 得到的项。例如：

  $$(\lambda x.x)y\rightarrow y\\ (\lambda x.x(\lambda x.x))(u\;r)\rightarrow(u\;r)(\lambda x.x)$$

  （其中第二个式子实际上是用$(u\;r)$ 去代换$x(\lambda x.x)$ 中所有自由的 x，即为$(u\;r)(\lambda x.x)$。）

• 考虑项：

  $$(\lambda x.x)((\lambda x.x)(\lambda z.(\lambda x.x)z))$$

  记$\lambda x.x=id$，即$\forall t,(\lambda x.x)t=idt\rightarrow t$。即为：

  $$id(id(\lambda z.idz))$$

  在全 beta 归约下，任何时刻可以归约任何一个约式。可以选择：

  • 从内到外归约：

    $$id(id(\lambda z.idz))\\ \rightarrow id(id(\lambda z.z))\\ \rightarrow id(\lambda z.z)\\ \rightarrow \lambda z.z$$

  • 从外到内归约：

    $$id(id(\lambda z.idz))\\ \rightarrow id(\lambda z.idz)\\ \rightarrow \lambda z.idz\\ \rightarrow \lambda z.z$$

  • 我们也可以不允许抽象内部的归约。即$\lambda z.idz$ 已经作为一个范式，而不对$\lambda z.$ 抽象内部进行归约。当然应该从外到内归约：

    $$id(id(\lambda z.idz))\\ \rightarrow id(\lambda z.idz)\\ \rightarrow \lambda z.idz$$

# lambda 演算中的程序设计

我理解的 lambda 演算实际上还是在描述函数。譬如$\lambda x.x+1$，其中 λ 跟着的是函数参数，“.” 后面跟着函数的内容。然后如果传入一个参数，即作用于 a 时，就会求值得到用 a 去替换函数内容中的自变量 x。

• 如果想描述的函数有多自变量怎么办？$\lambda(x,y).s$。实际上，我们可以写为$\lambda x.\lambda y.s$，这样先传入 y 的值，然后会继续得到一个 lambda 抽象（函数），再求值。譬如：

  $$\lambda(x,y).x+y\\ (\lambda x.\lambda y.x+y)3\;4\\ \rightarrow(\lambda x.x+3)\;4\\ \rightarrow 4+3$$

# Church 布尔式

• 定义：

  $$tru=\lambda t.\lambda f.t\\ fls=\lambda t.\lambda f.f\\ test=\lambda l.\lambda m.\lambda n.l\;m\;n$$

  为什么要定义这些东西？实际上，它用函数来描述了 if 语句：

  $$test\;tru\;v\;w\\ =(\lambda l.\lambda m.\lambda n.l\;m\;n)tru\;v\;w\\ \rightarrow(\lambda m.\lambda n.tru\;m\;n)v\;w\\ \rightarrow(\lambda n.tru\;v\;n)w\\ \rightarrow tru\;v\;w\\ =(\lambda t.\lambda f.t)v\;w\\ \rightarrow(\lambda f.v)w\\ \rightarrow v$$

  $$test\;fls\;v\;w\\ =(\lambda l.\lambda m.\lambda n.l\;m\;n)fls\;v\;w\\ \rightarrow(\lambda m.\lambda n.fls\;m\;n)v\;w\\ \rightarrow(\lambda n.fls\;v\;n)w\;\\ \rightarrow fls\;v\;w\\ =(\lambda t.\lambda f.f)v\;w\\ \rightarrow(\lambda f.f)w\\ \rightarrow w$$

  实际上，$tru\;v\;w$ 可以归约到$w$，$fls\;v\;w$ 可以归约到$w$。我们用 test 可以判断布尔的真假。即

  $test\;b\;v\;w$ 如果归约到 v 了 b 就为真，否则为假。

• 我们可以定义逻辑联结词：

  $$and=\lambda b.\lambda c.b\;c\;fls$$

  它的作用是：

  $$and\;tru\;tru\\ =(\lambda b.\lambda c.b\;c\;fls)tru\;tru\\ \rightarrow (\lambda c.tru\;c\;fls)tru\\ \rightarrow tru\;tru\;fls\\ \rightarrow tru\\ and\;fls\;tru\rightarrow fls$$

  同理：

  $$or=\lambda b.\lambda c.b\;tru\;c\\ not=\lambda b.b\;fls\;tru$$

• 我们能定义值得序对为项：

  $$pair=\lambda f.\lambda s.\lambda b.b\;f\;s\\ fst=\lambda p.p\;tru\\ snd=\lambda p.p\;fls$$

  有：

  $$fst(pair\;v\;w)\\ =fst((\lambda f.\lambda s.\lambda b.b\;f\;s)v\;w)\\ \rightarrow fst(\lambda b.b\;v\;w)\\ =(\lambda p.p\;tru)\;(\lambda b.b\;v\;w)\\ \rightarrow (\lambda b.b\;v\;w)\;tru\\ \rightarrow tru\;v\;w\\ \rightarrow v$$

# Church 数值

• 定义 Church 数值：

  $$c_0=\lambda s.\lambda z.z\\ c_1=\lambda s.\lambda z.s\;z\\ c_2=\lambda s.\lambda z.s\;(s\;z)\\ c_3=\lambda s.\lambda z.s\;(s\;(s\;z))\\ .......$$

  $$succ=\lambda n.\lambda s.\lambda z.s\;(n\;s\;z)\\ succ\;c_3=(\lambda n.\lambda s.\lambda z.s\;(n\;s\;z))c_3\\ \rightarrow\lambda s.\lambda z.s\;(c_3\;s\;z)\\ =\lambda s.\lambda z.s\;([\lambda s.\lambda z.s(s(s\;z))]s\;z)\\ \rightarrow\lambda s.\lambda z.s([\lambda z.s(s(s\;z))]z)\\ \rightarrow\lambda s.\lambda z.s(s(s(s\;z)))=c_4$$

  这里解释下。还记得抽象式中，$\lambda s.\lambda z.s\;z$ 中 s 和 z 都表示了函数的内容。我们可以理解 s 为一个 “后继函数”。可以记$c_n=\lambda s.\lambda z.s^n\;z$。求值为$c_n\;a\;b\rightarrow a^n\;b$。

  那么后继函数实际上就是用了这个求值，使得$s\;(c_n\;s\;z)\rightarrow s\;(s^n\;z)=s^{n+1}\;z$。

• 定义加法：

  $$plus=\lambda m.\lambda n.\lambda s.\lambda z.m\;s\;(n\;s\;z)\\$$

  只看函数内容$m\;s\;(n\;s\;z)$，因为求值有：

  $$c_a\;s\;(c_b\;s\;z)\rightarrow s^a\;(c_b\;s\;z)\rightarrow s^a\;(s^b\;z)=s^{a+b}\;z$$

  所以有$plus\;c_n\;c_m\rightarrow c_{n+m}$。

  定义乘法：

  $$times=\lambda m.\lambda n.m\;(plus\;n)\;c_0$$

  只看函数内容$m\;(plus\;n)\;c_0$，因为有：

  $$c_a\;(plus\;c_b)\;c_0\rightarrow (plus\;c_b)^a\;c_0=plus\;c_b\;(plus\;c_b\;(...\;plus\;c_b\;c_0))))\\ \rightarrow c_{a\times b}$$

  因为实际上就是把$c_b$ 往$c_0$ 上加了 a 次。

• 定义判零：

  $$iszro=\lambda m.m\;(\lambda x.fls)\;tru\\ iszro\;c_0\rightarrow c_0\;(\lambda x.fls)\;tru\\$$

  \rightarrow(\lambda z.z);tru\
  \rightarrow tru\
  iszro;c_n\rightarrow c_n;(\lambda x.fls);tru\
  =(\lambda s.\lambda z.s^n;z)(\lambda x.fls);tru\
  \rightarrow (\lambda z.(\lambda x.fls)^n;z);tru\
  \rightarrow (\lambda x.fls)^n tru\
  \rightarrow fls\

  $$返回值也是个Church布尔值。$$

  $$zz=pair\;c_0\;c_0\\ ss=\lambda p.pair\;(snd\;p)\;(plus\;c_1\;(snd\;p))\\ prd=\lambda m.fst\;(m\;ss\;zz)$$

  为什么它可以实现前趋呢？不难发现，$prd\;c_n\rightarrow fst\;(ss^n\;zz)$

  而$ss\;zz$ 求值其实等于$pair\;c_0\;c_1$。然后$ss^2\;zz=pair\;c_1\;c_2$。因此$ss^n\;zz=pair\;c_{n-1}\;c_n$。

  所以$prd\;c_n\rightarrow fst\;(pair\;c_{n-1}\;c_n)\rightarrow c_{n-1}$。

• 定义减法：

  $$minus=\lambda m.\lambda n.n\;prd\;m\\ minus\;c_a\;c_b\rightarrow c_b\;prd\;c_a\rightarrow prd^b\;c_a\rightarrow c_{a-b}$$

• 定义判等：

  $$equal=\lambda m.\lambda n.iszro(minus\;m\;n)$$

# 丰富演算 ——Church 编码和真实值的转换

• 可以定义抽象，使其可以将 Church 布尔式转化为之前无类型算术表达式中真正的布尔式：

  $$realbool=\lambda b.b\;true\;false\\ realbool\;tru\rightarrow true;\\ realbool fls\rightarrow false;$$

  同理可以反过来转换：

  $$churchbool=\lambda b.if\;b\;then\;tru\;else\;fls\\ churchbool\;true\rightarrow if\;true\;then\;tru\;else\;fls\rightarrow tru\\ churchbool false\rightarrow fls$$

  这里的推导，既可以根据 λ 演算的规则，也可以根据无类型算术表达式的推导规则。

  同样也可以定义，真正判等：（我们如果带了个真正，就表示求值是个 true 或 false，而不是 Church 编码的布尔式）

  $$realeq=\lambda m.\lambda n.realbool(equal\;m\;n)$$

  Church 数值转真正数值：

  $$realnat=\lambda m.m\;(\lambda x.succ\;x)\;0\\ realnat\;c_3\rightarrow succ\;succ\;succ\;0=3$$

  我们不能直接定义$realnat=\lambda m.m\;succ\;0$，因为$succ$ 只是一个标识而本身没有语法意义。因此我们需要把它包装在一个小函数中，而不能直接当作一个函数来用。

# 递归

• 有些抽象在归约时，仍是他自己。譬如：

  $$omega=(\lambda x.x\;x)(\lambda x.x\;x)$$

• 不动点组合式：

  $$fix=\lambda f.(\lambda x.f\;(\lambda y.x\;x\;y))(\lambda x.f\;(\lambda y.x\;x\;y))$$

  这有啥用呢？实际上，它可以解决递归问题。用最简单的阶乘函数来考虑下：

  $$g=\lambda fct.\lambda n.if\;realeq\;n\;c_0\;then\;c_1\;else\;(times\;n\;(fct\;(prd\;n)))\\ factorial=fix\;g$$

  先定义$g=\lambda f.<...>$，$<...>$ 内为函数内容。然后再定义$F=fix\;g$。

  以一个例子，考虑下$factorial\;c_3$：

  $$factorial\;c_3=fix\;g\;c_3\\ \rightarrow h\;h\;c_3\quad (h:=\lambda x.g\;(\lambda y.x\;x\;y))\\ \rightarrow g\;fct\;c_3\quad(fct:=\lambda y.h\;h\;y)\\ \rightarrow \lambda n.if\;realeq\;n\;c_0\;then\;c_1\;else\;(times\;n\;(fct\;(prd\;n)))\;c_3\\ \rightarrow if\;realeq\;c_3\;c_0\;then\;c_1\;else\;(times\;c_3\;(fct\;(prd\;c_3)))\\ \rightarrow^*times\;c_3\;(fct\;(prd\;c_3))\\ \rightarrow^* times\;c_3\;fct\;c_2\\ \rightarrow^* times\;c_3\;(g\;fct\;c_2)\\ \rightarrow^* times\;c_3\;(if\;realeq\;c_2\;c_0\;then\;c_1\;else\;times\;c_2\;(fct(prd\;c_2)))\\ \rightarrow^* times\;c_3\;(times\;c_2\;c_1)\\ \rightarrow^* c_6$$

  其中关键在于：

  $$fct\;c_2\rightarrow h\;h\;c_2\rightarrow g\;(\lambda y.h\;h\;y)\;c_2\rightarrow g\;fct\;c_2$$

  即$fct$ 是自重复的。

# 形式化定义

其实前面已经用半天了，又回来形式化定义下。

• 定义项的自由变量，记为$FV(t)$，定义如下：

  $$FV(x)=\{x\}\\ FV(\lambda x.t_1)=FV(t_1)-\{x\}\\ FV(t_1\;t_2)=FV(t_1)\cup FV(t_2)$$

• 关于代入，首先，我们约定只是囿变量名称不同的项在所有上下文中可交替使用。即可以 “换名”：

  $$\lambda x.x+y=\lambda w.w+y$$

  对代换的定义为：

  $$[x\mapsto s]x=s\\ [x\mapsto s]y=y\quad if\;y\neq x\\ [x\mapsto s](\lambda y.t_1)=\lambda y.[x\mapsto s]t_1\quad if\;y\neq x\;and\;y\notin FV(s)\\ [x\mapsto s](t_1\;t_2)=([x\mapsto s]t_1)([x\mapsto s]t_2)$$

  其中，第三行可以先把 y 换名换成满足条件的。

• lambda 演算语义的定义：

  $$\frac{t_1\rightarrow t_1'}{t_1\;t_2\rightarrow t_1'\;t_2}\\ \frac{t_2\rightarrow t_2'}{v_1\;t_2\rightarrow v_1\;t_2'}\\ (\lambda x.t_{12})\;v_2\rightarrow [x\mapsto v_2]t_{12}$$

# 项的无名称表示

# 项和上下文

• 对每个 λ 抽象，我们可以找到对应的 de Bruijn 项，即去掉囿变量，用数字替换：

  $$\lambda z.(\lambda y.y\;(\lambda x.x))\;(\lambda x.z\;x)=\lambda.(\lambda.1\;(\lambda.1))(\lambda.2\;1)$$

  而书上是从 0 开始标号的。

  然后自由变量的话，可以用大于囿变量个数的自然数代换它。

• 形式化的，定义无名项：

  设$\mathcal{T}$ 是最小的集簇$\{\mathcal{T_0},\mathcal{T_1},...\}$，使得：

  • $\forall 0\leq k< n,k\in\mathcal{T}_n$。
  • 如果$t_1\in\mathcal{T}_n,\lambda.t_1\in\mathcal{T}_{n-1}$。
  • 如果$t_1,t_2\in\mathcal{T}_n$，那么$t_1\;t_2\in\mathcal{T}_n$。

  仔细想一想，可以发现$\mathcal{T}_n$ 为至多含有 n 个自由变量的项。例如$\lambda .5\;0\in\mathcal{T}_{6}$，5 为自由变量。

• 我们可以对所有的 de Bruijn 变量指派一个 de Bruijn 索引（称为一个命名的上下文），例如：

  $$\Gamma=x\mapsto 4\\y\mapsto 3\\z\mapsto 2\\ a\mapsto 1\\b\mapsto 0$$

  那么$a\;\lambda x.a=1\;\lambda.2$。注意自由变量的索引需要加上非自由变量的个数。

  上面那个指派也可以简写为$\Gamma=x,y,z,a,b$

# 移位和代换

• 定义移位：

  $$\uparrow^d_c(k)=\begin{cases}k&if\;k<c\\k+d&if\;k\geq c\end{cases}\\ \uparrow^d_c(\lambda.t_1)=\lambda.\uparrow^d_{c+1}(t_1)\\ \uparrow^d_c(t_1\;t_2)=\uparrow^d_c(t_1)\;\uparrow^d_c(t_2)$$

  默认从 0 开始移位，例：

  $$\uparrow^2(\lambda.0\;1\;(\lambda.0\;1\;2))=\lambda.\uparrow^2_10\;1\;(\lambda.0\;1\;2)\\ =\lambda.0\;\uparrow^2_11\;(\lambda.0\;1\;2)\\ =\lambda.0\;3\;(\lambda.\uparrow^2_2 0\;1\;2)\\ =\lambda.0\;3\;(\lambda.0\;1\;4)$$

• 定义代换：

  $$[j\mapsto s]k=\begin{cases}s&if\;k=j\\k&else\end{cases}\\ [j\mapsto s](\lambda.t_1)=\lambda.[j+1\mapsto \uparrow^1 s]t_1\\ [j\mapsto s](t_1\;t_2)=[j\mapsto s]t_1\;[j\mapsto s]t_2$$

  譬如对全局上下文$\Gamma=a,b$，有

  $$[b\mapsto a\;(\lambda z.a)](b\;(\lambda x.b))=[0\mapsto 1\;(\lambda.2)](0\;(\lambda.1))\\ =(1\;\lambda.2)\;[0\mapsto 1\;(\lambda.2)](\lambda.1)\\ =(1\;\lambda.2)\;\lambda.[0+1\mapsto\uparrow^1_0(1\;\lambda.2)]1\\ =(1\;\lambda.2)\;\lambda.[1\mapsto(2\;\lambda.3)]1\\ =(1\;\lambda.2)\;\lambda.(2\;\lambda.3)\\ =(a\;\lambda z_1.a)\;(\lambda z_2.a\;\lambda z_3.a)$$

# 求值

$$\frac{t_1\rightarrow t_1'}{t_1\;t_2\rightarrow t_1'\;t_2}\\ \frac{t_2\rightarrow t_2'}{v_1\;t_2\rightarrow v_1\;t_2'}\\ (\lambda.t_{12})\;v_2\rightarrow \uparrow^{-1}_0([0\mapsto\uparrow^1_0 v_2]t_{12})$$

例如

$$(\lambda.1\;0\;2)(\lambda.0)\rightarrow 0\;(\lambda.0)\;1$$

而不是$1\;(\lambda.0)\;2$，因为需要对自由变量重新编排。

# 简单类型

# 类型算术表达式

# 类型关系

• 语法定义：

  $$T::=Bool\\ --------------\\ true:Bool\\ false:Bool\\ \frac{t_1:Bool\quad t_2:T\quad t_3:T}{if\;t_1\;then\;t_2\;else\;t_3:T}\\ --------------\\ T::=Nat\\ --------------\\ 0:Nat\\ --------------\\ \frac{t_1:Nat}{succ\;t_1:Nat}\\ \frac{t_1:Nat}{pred\;t_1:Nat}\\ \frac{t_1:Nat}{iszro\;t_1:Bool}\\$$

  注，T 表示类型。而 if 语句里表示$t_2,t_3$ 和 if 语句最后都是同一类型。（而非必须是 Bool，只是目前我们类型只定义了 Bool）

• 定义，形式地，算术表达式的类型关系是项和类型之间的最小二元关系。如果存在某个 T，使得$t:T$，则称项 t 是可类型化的，或良类型的。

• 定理，如果一个项是可类型化的，那么它的类型是唯一的。（t 的生成树唯一。）

# 安全性 = 进展 + 保持

• 进展：一个良类型的项不会受阻。（要么它是一个值，要么它根据求值规则做下一步）

  保持：一个良类型的项做一步求值，所得的项仍是良类型的。

# 简单类型的 lambda 演算

• 定义，类型 Bool 上的简单类型集合是由下列语法产生的：

  $$T::=Bool|T\rightarrow T$$

  类型构造子$\rightarrow$ 是右结合的。可以把它理解为 “函数类型”。譬如$Bool\rightarrow Bool$ 就是一个布尔到布尔的函数类型，可以说$\lambda x.true:Bool\rightarrow Bool$。

• 我们可以对抽象确定参数类型：$\lambda x:T.t$，其中相当于要求了函数的自变量（参数）x 是 T 类型的。

• 像上面直接用注释的形式$t:T$ 标出项的类型的语言称为显式类型化语言。要求类型检查其自己推导类型的称为隐式类型化语言。显然我们主要讨论前者。

• 定义抽象类型的推导规则：

  $$\frac{x:T_1\vdash t_2:T_2}{\vdash \lambda x:T_1:t_2:T_1\rightarrow T_2}$$

  中文说就是，如果确定参数 x 的类型为$T_1$ 可以推导出函数体$t_2$ 会返回一个$T_2$ 类型的话，那么抽象$\lambda x:T_1:t_2$ 也可以被推导出是一个$T_1\rightarrow T_2$ 的函数。

• 定义，一个类型环境（或称类型化的上下文）$\Gamma$ 是一个 变量 + 类型的序列。而逗号表示引入新的变量 + 类型来扩展$\Gamma$。

  譬如：$\Gamma:\{x:Nat\}$，则有$\Gamma\vdash iszro(x):Bool$。相当于整了个假设大前提。显然$\emptyset\vdash\{true:Bool\}$，可以简写省略空集符号。

  我们用$dom(\Gamma)$ 表示$\Gamma$ 中规定了类型的变量的集合。

• 抽象的类型规则一般表示为：

  $$\frac{\Gamma,x:T_1\vdash t_2:T_2}{\Gamma\vdash\lambda x:T_1.t_2:T_1\rightarrow T_2}\quad (T-Abs)$$

  中文说就是，如果$\Gamma\cup\{x:T_1\}$ 下可以推出$t_2:T_2$，那么$\Gamma$ 下就可以推出$\lambda x:T_1.t_2:T_1\rightarrow T_2$。

• 根据定义，也有：

  $$\frac{x:T\in\Gamma}{\Gamma\vdash x:T}\quad(T-Var)$$

  前提$x:T\in\Gamma$ 读作 “在$\Gamma$ 中假设 x 的类型为 T”。

• 定义应用的类型规则：

  $$\frac{\Gamma\vdash t_1:T_1\rightarrow T_2\quad\Gamma\vdash t_2:T_1}{\Gamma\vdash t_1\;t_2:T_2}\quad(T-App)$$

---

• 纯简单类型 lambda 演算的语法定义：

  $$t::=x|\lambda x:T.t|t\;t\\ v::=\lambda x:T.t\\ T::=T\rightarrow T\\ \Gamma::=\emptyset|\Gamma,x:T$$

  语义定义：

  $$\frac{t_1\rightarrow t_1'}{t_1\;t_2\rightarrow t_1'\;t_2}\quad(E-App_1)\\ \frac{t_2\rightarrow t_2'}{v_1\;t_2\rightarrow v_1\;t_2'}\quad(E-App_2)\\ (\lambda x:T_1.t_1)\;v_2\rightarrow [x\mapsto v_2]t_1\quad(E-AppAbs)\\ \frac{x:T\in\Gamma}{\Gamma\vdash x:T}\quad(T-Var)\\ \frac{\Gamma,x:T_1\vdash t_2:T_2}{\Gamma\vdash\lambda x:T_1.t_2:T_1\rightarrow T_2}\quad (T-Abs)\\ \frac{\Gamma\vdash t_1:T_1\rightarrow T_2\quad\Gamma\vdash t_2:T_1}{\Gamma\vdash t_1\;t_2:T_2}\quad(T-App)\\$$

  我们用$\lambda_\rightarrow$ 来表示简单类型的 lambda 演算。

# 类型的性质

• 定理，类型唯一性：在一个给定的类型环境$\Gamma$ 中，一个项 t ($FV(t)\in dom(\Gamma)$)，至多有一个类型。

• 定理 [进展]：若 t 是一个封闭的，良类型的项（即存在 T，使得$\vdash t:T$），则 t 要么是一个值，要么存在$t'$ 使$t\rightarrow t'$。

• 引理 [置换]：如果$\Gamma\vdash t:T$，$\Delta$ 是$\Gamma$ 的一个置换，则$\Delta\vdash t:T$。（感觉是废话，因为集合是无序的）

• 引理 [弱化]：如果$\Gamma\vdash t:T$ 且$x\notin dom(\Gamma)$，则$\Gamma,x:S\vdash t:T$。（即加了个没用的绑定）

• 引理 [类型在代换下保持]：如果$\Gamma,x:S\vdash t:T$ 且$\Gamma\vdash s:S$，则$\Gamma\vdash[x\mapsto s]t:T$。

• 定理 [保持]：如果$\Gamma\vdash t:T$ 且$t\rightarrow t'$，则$\Gamma\vdash t':T$。

# Curry-Howard 对应

• 关于$T_1\rightarrow T_2$ 这样的类型有两种类型规则：

  • 引入规则（T-Abs），描述该类型的元素是如何产生的。
  • 消去规则（T-App），描述该类型的元素是如何使用的。

• Curry-Howard 对应（Curry-Howard 同构）：

  逻辑	程序语言
  命题	类型
  命题$P\supset Q$	类型$P\rightarrow Q$
  命题$P\wedge Q$	类型$P\times Q$
  命题 P 的证明	类型 P 的一个项 t
  命题 P 是可证明的	有一个项 t 是类型 P 的

# 抹除和类型性

• 可以定义 erase 函数去抹除对项的类型注释：

  $$erase(x)=x\\ erase(\lambda x:T_1.t_2)=\lambda x.erase(t_2)\\ erase(t_1\;t_2)=erase(t_1)\;erase(t_2)$$

• 定理，若$t\rightarrow t'$，则$erase(t)\rightarrow erase(t')$。若$erase(t)\rightarrow m$，则存在$t'$，使得$t\rightarrow t',erase(t')=m$。

• 定义，无类型 lambda 演算中一个项 m，如果存在某个简单类型项 t，类型 T 和上下文$\Gamma$ 使得$erase(t)=m$ 且$\Gamma\vdash t:T$，则 m 在$\lambda_\rightarrow$ 中是可类型化的。

# 简单扩展

• 我们用 A 表示基本类型（String，Float，Nat，Bool 等），用 Unit 表示单位类型。于是有扩展：

  $$T::=...|A|Unit\\ t::=...|unit\\ v::=...|unit\\ ----------------\\ \Gamma\vdash unit:Unit\\ t_1;t_2=(\lambda x:Unit.t_2)\;t_1,x\notin FV(t_2)$$

  Unit 的作用类似于 C 和 Java 中的 void 类型。

# 序列和通配符

• 定义序列：$t::=...|t_1;t_2$

• 定义对序列$t_1;t_2$ 的求值规则和类型规则：

$$\frac{t_1\rightarrow t_1'}{t_1;t_2\rightarrow t_1';t_2}\quad(E-Seq)\\ unit;t_2\rightarrow t_2\\ \frac{\Gamma\vdash t_1:Unit\quad \Gamma\vdash t_2:T_2}{\Gamma\vdash t_1;t_2:T_2}\quad(T-Seq)$$

​ 这时候，会发现这个求值规则实际上是符合$t_1;t_2=(\lambda x:Unit.t_2)\;t_1$ 的定义的。我们可以把序列看作这样一个 λ 抽象的缩写。

• 定理，用$\lambda^E$ 表示带序列的简单类型 lambda 演算，$\lambda^I$ 表示只带 Unit 类型的简单类型 lambda 演算。

  设$e\in\lambda^E\rightarrow\lambda^I$，e 表示用$(\lambda x:Unit.t_2)\;t_1$ 去替换$t_1;t_2$。于是对$\lambda^E$ 中的每个项，都有：

  • $t\rightarrow_E t'$ 当且仅当$e(t)\rightarrow_I e(t')$。
  • $\Gamma\vdash^E t:T$ 当且仅当$\Gamma\vdash^I e(t):T$。

  其实序列是我们写程序时常用的顺序结构。上述定理说明了序列可以用更基本的类型和求值行为推导出。注意到我们用$\lambda^I$ 去替换序列时，有要求$x\notin FV(t_2)$，所以有时候也会写成$(\lambda\_:Unit.t_2)\;t_1$，

# 归属

• 定义 “将类型 T 归属到项 t”：

  $$t::=...|t\;as\;T$$

• 定义对应的求值规则：

  $$v_1\;as\;T\rightarrow v_1\quad(E-Ascribe)\\ \frac{t_1\rightarrow t_1'}{t_1\;as\;T\rightarrow t_1'\;as\;T}\quad (E-Ascribe1)\\$$

• 定义对应的类型规则：

  $$\frac{\Gamma\vdash t_1:T}{\Gamma\vdash t_1\;as\;T:T}\quad(T-Ascribe)$$

归属可以用来做 typedef。譬如：

$$UU\;as\;Unit\rightarrow Unit;\\ (\lambda f:UU.f\;unit)(\lambda x:Unit.x);$$

就可以很容易推导出：$(\lambda f:UU.f\;unit)(\lambda x:Unit.x):Unit$

# let 绑定

• 语法定义：

  $$t::=...|let\;x=t\; in\;t$$

• 求值规则：

  $$let\;x=v_1\;in\;t_2\rightarrow [x\mapsto v_1]t_2\quad(E-LETV)\\ \frac{t_1\rightarrow t_1'}{let\;x=t_1\;in\;t_2\rightarrow let\;x=t_1'\;in\;t_2}\quad(E-LET)$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_1\quad\Gamma,x:T_1\vdash t_2:T_2}{let\;x=t_1\;in\;t_2:T_2}\quad(T-LET)$$

这东西的理解，首先应该把它看成$let\;(x=t_1)\;in\;t_2$，意思为在表达式$t_2$ 中，绑定$x$ 为$t_1$ 的求值。譬如$let\;x=3+5\;in\;x-2$。

也可以用一个 lambda 抽象来等价地表示它：$let\;x=t_1\;in\;t_2=(\lambda x:T_1.t_2)\;t_1$。

在出现 let 绑定时，类型检查器一定会有一个推导：

$$\frac{\frac{...}{\Gamma\vdash t_1:T_1}\quad\frac{...}{\Gamma,x:T_1\vdash t_2:T_2}}{let\;x=t_1\;in\;t_2:T_2}\quad(T-LET)$$

这个推导就对应了 lambda 抽象的一个推导：

$$\frac{\frac{\frac{...}{\Gamma,x:T_1\vdash t_2:T_2}}{\Gamma\vdash\lambda x:T_1.t_2:T_1\rightarrow T_2}\quad\frac{...}{\Gamma\vdash t_1:T_1}}{\Gamma\vdash(\lambda x:T_1.T_2)\;t_1:T_2}$$

# 序对

• 语法定义：

  $$t::=...|\{t,t\}|t.1|t.2\\ v::=...|\{v,v\}\\ T::=T_1\times T_2$$

• 求值规则：

  $$\{v_1,v_2\}.1\rightarrow v_1\quad(E-PAIRBETA1)\\ \{v_1,v_2\}.2\rightarrow v_2\quad(E-PAIRBETA2)\\ \frac{t_1\rightarrow t_1'}{t_1.1\rightarrow t_1'.1}\quad(E-PROJ1)\\ \frac{t_1\rightarrow t_1'}{t_1.2\rightarrow t_1'.2}\quad(E-PROJ2)\\ \frac{t_1\rightarrow t_1'}{\{t_1,t_2\}\rightarrow\{t_1',t_2\}}\quad(E-PAIR1)\\ \frac{t_2\rightarrow t_2'}{\{v_1,t_2\}\rightarrow\{v_1,t_2'\}}\quad(E-PAIR2)$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_1\quad \Gamma\vdash t_2:T_2}{\Gamma\vdash\{t_1,t_2\}:T_1\times T_2}\quad(T-PAIR)\\ \frac{\Gamma\vdash t_1:T_1\times T_2}{\Gamma\vdash t_1.1:T_1}\quad(T-PROJ1)\\ \frac{\Gamma\vdash t_1:T_1\times T_2}{\Gamma\vdash t_1.2:T_2}\quad(T-PROJ2)\\$$

  这就是平常用的 C++ 里的 pair。用它可以扩展成元组，数组。要注意的是，无论求 1 还是 2，或者代入函数时，都必须把两项都算出值：

  $$(\lambda x:Nat\times Nat.x.2)\{pred\;4,pred\;5\}\\ \rightarrow(\lambda x:Nat\times Nat.x.2)\{3,pred\;5\}\\ \rightarrow(\lambda x:Nat\times Nat.x.2)\{3,4\}\\ \rightarrow\{3,4\}.2\\ \rightarrow 2$$

# 元组

• 语法定义：

  $$t::=...|\{t_i,i\in1..n\}|t.i\\ v::=\{v_i,i\in1..n\}\\ T::=\{T_i,i\in1..n\}$$

• 求值规则：

  $$\{v_i,i\in1..n\}.j\rightarrow v_j\\ \frac{t_1\rightarrow t_1'}{t_1.i\rightarrow t_1'.i}\\ \frac{t_j\rightarrow t_j'}{\{v_i,i\in1..j-1,v_j,v_i,i\in j+1..n\}\rightarrow\{v_i,i\in1..j-1,v_j',v_i,i\in j+1..n\}}$$

• 类型规则：

  $$\frac{foreach\;i,\Gamma\vdash t_i:T_1}{\Gamma\vdash\{t_i,i\in1..n\}:\{T_i,i\in1..n\}}\\ \frac{\Gamma\vdash t_1:\{T_i,i\in 1..n\}}{\Gamma\vdash t_1.j:T_j}$$

  这就是最常用的元组类型（允许不同类型放在一起）。实例：

  $$\{1,2,3,true,false\}$$

# 记录

• 语法定义

  $$t::=...|\{l_i=t_i,i\in1..n\}|t.l\\ v::=...|\{l_i=v_i,i\in 1..n\}\\ T::=...|\{l_i:T_i,i\in 1..n\}$$

• 求值规则

  $$\{l_i=v_i,i\in1..n\}.l_j\rightarrow v_j\\ \frac{t_1\rightarrow t_1'}{t_1.l\rightarrow t_1'.l}\\ \frac{t_j\rightarrow t_j'}{\{l_i=v_i,i\in 1..j-1,l_j=t_j,l_i=t_i,i\in j+1..n\}\rightarrow\{l_i=v_i,i\in 1..j-1,l_j=t_j',l_i=t_i,i\in j+1..n\}}$$

  注意这里面从左到右求值的含义，左侧都是值了，才能求值。

• 类型规则

  $$\frac{foreach\;i,\Gamma\vdash t_i:T_i}{\Gamma\vdash\{l_i=t_i,i\in1..n\}:\{l_i:T_i,i\in1..n\}}\\ \frac{\Gamma\vdash t_1:\{l_i:T_i,i\in1..n\}}{\Gamma\vdash t_1.l_j:T_j}$$

这其实有些类似 map。但是它支持了不同类型放在一起。给出实例一个：

$$\{patato:100,tomato:true\}:\{patato:Nat,tomato:Bool\}$$

# 和

• 语法定义：

  $$t::=...|inl\;t|inr\;t|(case\;t\;of\;inl\;x\Rightarrow t|inr\;x\Rightarrow t)\\ v::=...|inl\;v|inr\;v\\ T::=...|T+T$$

• 求值规则：

  $$case\;(inl\;v_0)\;of\;inl\;x_1\Rightarrow t_1|inr\;x_2\Rightarrow t_2\\ \rightarrow[x_1\mapsto v_0]t_1\\ case\;(inr\;v_0)\;of\;inl\;x_1\Rightarrow t_1|inr\;x_2\Rightarrow t_2\\ \rightarrow[x_2\mapsto v_0]t_2\\ \frac{t_0\rightarrow t_0'}{case\;t_0\;of\;inl\;x_1\Rightarrow t_1|inr\;x_2\Rightarrow t_2\rightarrow case\;t_0'\;of\;inl\;x_1\Rightarrow t_1|inr\;x_2\Rightarrow t_2}\\ \frac{t_1\rightarrow t_1'}{inl\;t_1\rightarrow inl\;t_1'}\\ \frac{t_1\rightarrow t_1'}{inr\;t_1\rightarrow inr\;t_1'}$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_1}{\Gamma\vdash inl\;t_1:T_1+T_2}\\ \frac{\Gamma\vdash t_1:T_2}{\Gamma\vdash inr\;t_1:T_1+T_2}\\ \frac{\Gamma\vdash t_0:T_1+T_2\quad\Gamma,x_1:T_1\vdash t_1:T_1\quad\Gamma,x_2:T_2\vdash t_2:T_2}{\Gamma\vdash case\;t_0\;of\;inl\;x_1\Rightarrow t_1|inr\;x_2\Rightarrow t_2:T}$$

• 怎么理解这个类型呢？根据我的理解，这实际上是在 “取并集”。譬如两个记录类型：

  $$PhysicalAddr=\{firstlast:String,addr:String\}\\ VirtualAddr=\{name:String,email:String\}$$

  令$Addr=PhysicalAddr+VirtualAddr$。那么对于任意一个$Addr$ 类型的项 t，t 要么是 Physical 的，要么是 Virtual 的，因为它的生成规则一定是：

  $$t\equiv inl\;(t':PhysicalAddr):Addr\\ or\\ t\equiv inr\;(t':VirtualAddr):Addr$$

  就是对于两个不同的类型，把它们并起来获得一个新的大类型。但对这个大类型，我们又可以根据其中项究竟属于哪个小类型来操作：

  $$getName=\lambda a:Addr.case\;a\;of\;inl\;x\Rightarrow x.firstlast|inr\;y\Rightarrow y.name$$

  则$getName$ 是一个$Addr\rightarrow String$ 的函数，它的输入值相当于放宽了类型，无论是 Physical 还是 Virtual 都可以传进去，然后分类进行取 name。

• 此时其实会破坏类型的唯一性。即确定项$t=inl\;t':T_1$ 的类型不再唯一。例如$inl\;5$ 可以为$Nat+Nat$ 也可以为$Nat+Bool$。所以可以更改语法规则：

  $$t::=...|inl\;t\;as\;T|...$$

  这样要求了$inl\;t$ 的类型。$inl\;5\;as\;Nat+Nat$。然后求值和类型规则都需要重写。

# 变式

• 语法定义：

  $$t::=...|<l=t>\;as\;T|case\;t\;of\;<l_i=x_i>\Rightarrow t_i,i\in1..n\\ T::=...|<l_i:T_i>,in\in1..n$$

• 求值规则：

  $$case\;(<l_j=v_j>\;as\;T)\;of\;<l_i=x_i>\Rightarrow t_i,i\in1..n\rightarrow[x_j\mapsto v_j]t_j\\ \frac{t_0\rightarrow t_0'}{case\;t_0\;of\;<l_i=x_i>\Rightarrow t_i,i\in1..n\rightarrow case\;t_0'\;of\;<l_i=x_i>\Rightarrow t_i,i\in1..n}\\ \frac{t_i\rightarrow t_i'}{<l_i=t_i>\;as\;T\rightarrow <l_i=t_i'>\;as\;T}\\$$

• 类型规则：

  $$\frac{\Gamma\vdash t_j:T_j}{\Gamma\vdash<l_j=t_j>\;as\;<l_i:T_i>,i\in1..n:<l_i:T_i>,i\in1..n}\\ \frac{\Gamma\vdash t_0:<l_i:T_i>,i\in1..n\quad foreach\;i\;\Gamma,x_i:T_i\vdash t_i:T}{\Gamma\vdash case\;t_0\;of\;<l_i=x_i>\Rightarrow t_i,i\in 1..n:T}$$

• 变式实际上是和的推广。$inl\;t\;as\;T$ 扩展成了$<l_i=t_i>\;as\;T$。

  于是之前在和那里的例子可以为：

  $$Addr=<physical:PhysicalAddr,virtual:VirtualAddr>;\\$$

  那么 Addr 的一个实例 a，生成形式一定是：

  $$a\equiv <physical=t>\;as\;Addr\\ or\\ a\equiv <virtual=t>\;as\;Addr$$

  然后仍然可以 getName：

  $$getName=\lambda a:Addr.\\ case\;a\;of\\ <physical=x>\Rightarrow x.firstlast\\ |<virtual=y>\Rightarrow y.name$$

  则$getName:Addr\rightarrow String$。

• 此外，变式可以用来选值。考虑这样一个变式类型：

  $$OptionalNat=<none:Unit,some:Nat>$$

  于是实际上可以进行查询：

  $$query=\lambda a:OptionalNat.\\ case\;a\;of\\ <none=x>\Rightarrow-1\\ |<some=y>\Rightarrow y$$

  这实际上就是一个查询$query:OptionalNat\rightarrow Nat$，就是对$OptionalNat$ 类型的变量确定它究竟是个 Nat 还是个 Unit。这里 Optional 我认为理解为可以是若干类型中的一个。

• 还有单字段的变式：$<t_1:T_1>$。他有什么用呢？它可以用来区分 “不同意义的相同类型”。譬如，我的钱无论是美元，还是欧元，都可以用浮点数表示。那怎么区分它是欧元还是美元呢，实际上可以用单字段变式来定义新的类型，来加 “单位”：

  $$dollarAmount=<amount:Float>\\ euroAmout=<amount:Float>$$

  那么，美元转欧元的话，就必须输入是美元类型：

  $$dollar2euro=\lambda a:dollarAmount.\\ case\;a\;of\\ <amount=x>\Rightarrow <amount=times\;x\;1.03>\;as\;euroAmount\\ dollar2euro:dollarAmount\rightarrow euroAmount$$

# 枚举

• 枚举是变式的退化，其中每个字段都是 Unit 类型。譬如：

  $$Weekday=<monday:Unit,tuesday:Unit,wednesday:Unit,\\thursday:Unit,friday:Unit>$$

  然后譬如就可以有：

  $$nextBusinessDay=\lambda w:Weekday.\\ case\;w\;of\;<monday=x>\Rightarrow<tuesday=unit>\;as\;Weekday\\ |<tuesday=x>\Rightarrow<wednesday=unit>\;as\;Weekday\\ |<wednesday=x>\Rightarrow<thursday=unit>\;as\;Weekday\\ |<thursday=x>\Rightarrow<friday=unit>\;as\;Weekday\\ |<friday=x>\Rightarrow<monday=unit>\;as\;Weekday\\ nextBusinessDay:Weekday\rightarrow Weekday$$

# 一般递归

• 语法形式：

  $$t::=...|fix\;t$$

• 求值规则：

  $$fix\;(\lambda x:T_1.t_2)\rightarrow[x\mapsto(fix\;(\lambda x:T_1.t_2))]t_2\\ \frac{t_1\rightarrow t_1'}{fix\;t_1\rightarrow fix\;t_1'}$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_1\rightarrow T_1}{\Gamma\vdash fix\;t_1:T_1}$$

• 导出式：

  $$letrec\;x:T_1=t_1\;in\;t_2\\=_{def} let\;x=fix\;(\lambda x:T_1.t_1)\;in\;t_2$$

• 解释一下。fix 直接定义成了一个语法，并且给出了它的规则。fix 其实作用是给出函数的不动点。譬如$g:Nat\rightarrow Nat$，则$g\;(fix\;g)=fix\;g$。所以$g:(Nat\rightarrow Nat)\rightarrow Nat$。

  在之前，其实给出了无类型的 fix：

  $$fix=\lambda f.(\lambda x.f\;(\lambda y.x\;x\;y))(\lambda x.f\;(\lambda y.x\;x\;y))$$

  然而类型环境下是需要考虑不动点是否存在的。然后再写一个产生器。以阶乘为例：

  $$ff=\lambda g:Nat\rightarrow Nat.\lambda n:Nat.if\;iszro(n)\;then\;1\;else\;g(pred(n));\\ ff:(Nat\rightarrow Nat)\rightarrow Nat\rightarrow Nat$$

  那么 ff 的不动点是啥？实际上，就是$g=\lambda x:Nat.x!$。所以对 ff 求不动点，本质上就是把递归函数 g 的显形式解出来。

  $$F=fix\;ff\\ ff\;F=F$$

  当然，这个显形式如果$fix$ 就按上面的定义的话，本质就是一层一层展开，导致很长。

# 引用

# 基础

• 我们定义新算子 ref，表示为新的单元提供一个初始值：

  $$r=ref\;5;$$

  它的类型表示为：$r:Ref\;Nat$

• 同样可以定义反引用算子！：

  $$!r;\\ !(ref\;5):Nat$$

• 定义赋值算子：

  $$r:=7;$$

  整个赋值式的结果就是一个 Unit 类型（平凡类型）：

  $$(r:=7)\rightarrow unit:Unit$$

  回顾之前，其实赋值语句类型是 unit 很好地符合了 “序对” 的要求，即我们可以很好地顺序执行：

  $$(r:=7;!r)\rightarrow 7:Nat$$

  来替换：

  $$(\lambda\_:Unit.!r)(r:=succ(!r))\rightarrow 9:Nat$$

# 引用和别名

• 考虑引用 r，s：

  $$r=ref\;5;\\ s=r;$$

  则$s:Ref\;Nat$。而且他们指向同一单元。于是有：

  $$s:=83;\\ !r\rightarrow 83$$

  引用 r 和 s 称为是同一个单元的别名。

# 复合类型的引用

$$NatArray=Ref\;(Nat\rightarrow Nat)$$

表示数组类型。

$$newarray=\lambda\_Unit.ref\;(\lambda n:Nat.0)$$

然后$newarray\;unit;$ 就实现了新建一个全为 0 的数组的引用。

$$lookup=\lambda a:NatArray.\lambda n:Nat.(!a)\;n;$$

表示查询数组的第 n 位。

$$update=\lambda a:NatArray.\lambda m:Nat.\lambda v:Nat.\\ let\,oldf=!a\,in\\ a:=(\lambda n:Nat.if\ qual\ m\ n\ then\ v\ else\ oldf\ n);\\$$

$update:NatArray\rightarrow Nat\rightarrow Nat\rightarrow Unit$。是一个更新操作。

# 引用的类型规则

$$\frac{\Gamma\vdash t_1:T_1}{\Gamma:ref\ t_1:Ref\ T_1}\\ \frac{\Gamma\vdash t_1:Ref\ T_1}{\Gamma\vdash !t_1:T_1}\\ \frac{\Gamma\vdash t_1:Ref\ T_1\quad \Gamma\vdash t_2:Ref\ T_1}{\Gamma\vdash t_1:=t_2:Unit}$$

---

# 引用的规则汇总

• 定义一个存储$\mu$，表示存储单元到值得映射$\mu(l)=v$。一个类型上下文$\Gamma$。一个存储类型$\Sigma$ 是存储单元到类型得映射$\Sigma(l)=T$。如果有$dom(\mu)=dom(\Sigma)$ 且对每个$l\in dom(\mu),\Gamma|\Sigma\vdash\mu(l):\Sigma(l)$ 成立，则称$\mu$ 是良类型的，记为$\Gamma|\Sigma\vdash\mu$。一个存储$\mu$ 和一个存储类型$\Sigma$ 是一致的。

• 语法定义：

  t::=x|\lambda x:T.t|t\ t|unit|ref\ t|!t|t:=t|l\ v::=\lambda x:T.t|unit|l\\ T::=T\rightarrow T|Unit|Ref\ T\\ \Gamma::=\emptyset|\Gamma,x:T\\ \mu::=\emptyset|\mu,l=v\\ \Sigma::=\emptyset|\Sigma,l:T

  其中$l$ 表示存储位置，$\mu,l=v$ 表示新的存储绑定。

• 类型规则：

  $$\frac{x:T\in \Gamma}{\Gamma|\Sigma\vdash x:T}\\ \frac{\Gamma,x:T_1|\Sigma\vdash t_2:T_2}{\Gamma|\Sigma\vdash\lambda x:T_1.t_2:T_1\rightarrow T_2}\\ \frac{\Gamma|\Sigma\vdash t_1:T_1\rightarrow T_2\quad \Gamma|\Sigma\vdash t_2:T_1}{\Gamma|\Sigma\vdash t_1\ t_2:T_2}\\ \Gamma|\Sigma\vdash unit:Unit\\ \frac{\Sigma(l)=T_1}{\Gamma|\Sigma\vdash l:Ref\ T_1}\\ \frac{\Gamma|\Sigma\vdash t_1:T_1}{\Gamma|\Sigma\vdash ref\ t_1:Ref\ T_1}\\ \frac{\Gamma|\Sigma\vdash t_1:Ref\ T_1}{\Gamma|\Sigma\vdash !t_1:T_1}\\ \frac{\Gamma|\Sigma\vdash t_1:Ref\ T_1\quad\Gamma|\Sigma\vdash t_2:T_1}{\Gamma|\Sigma\vdash t_1:=t_2:Unit}$$

• 求值规则：

  $$\frac{t_1|\mu\rightarrow t_1'|\mu'}{t_1\ t_2|\mu\rightarrow t_1'\ t_2|\mu'}\\ \frac{t_1|\mu\rightarrow t_1'|\mu'}{v\ t_1|\mu\rightarrow v\ t_1'|\mu'}\\ (\lambda x:T_1.t_2)\ v_2|\mu\rightarrow[x\mapsto v_2]t_2|\mu\\ \frac{l\notin dom(\mu)}{ref\ v_1|\mu\rightarrow l|(\mu,l\mapsto v_1)}\\ \frac{t_1|\mu\rightarrow t_1'|\mu'}{ref\ t_1|\mu\rightarrow ref\ t_1'|\mu'}\\ \frac{\mu(l)=v}{!l|\mu\rightarrow v|\mu}\\ \frac{t_1|\mu\rightarrow t_1'|\mu'}{!t_1|\mu\rightarrow !t_1'|\mu'}\\ ......$$

  注意现在求值会附带个$\mu$，求值可能引起$\mu$ 的改变。

---

• 定理 [保持]：

  如果

  $$\Gamma|\Sigma\vdash t:T\\ \Gamma|\Sigma\vdash\mu\\ t|\mu\rightarrow t'|\mu'$$

  则对某个$\Sigma'\supseteq\Sigma$，有

  $$\Gamma|\Sigma'\vdash t':T\\ \Gamma|\Sigma'\vdash \mu'$$

  为什么会要求$\Sigma'\supseteq \Sigma$ 呢？因为对于一个新的项$t'$，他可能比 t 多的是一个$ref\ 10$ 的部分，那么根据求值规则就会：

  $$ref\ 10|\mu\rightarrow l|(\mu,l\mapsto 10)$$

  会扩大$\mu$，新分配一个地址 l。那么那 “某个$\Sigma'$” 就是$(\Sigma,l\mapsto T_1)$ 了。否则如果没有新开地址 l，那就可以是$\Sigma$。

• 引理 [代换]：

  如果

  $$\Gamma,x:S|\Sigma\vdash t:T\\ \Gamma|\Sigma\vdash s:S$$

  那么

  $$\Gamma|\Sigma\vdash[x\mapsto s]t:T$$

• 引理：

  如果

  $$\Gamma|\Sigma\vdash\mu\\ \Sigma(l)=T\\ \Gamma|\Sigma\vdash v:T$$

  那么

  $$\Gamma|\Sigma\vdash[l\mapsto v]\mu$$

• 定理 [进展]：

  如果

  t 是一个封闭的、良类型的项（即对某个 T 和$\Sigma$，有$\emptyset|\Sigma\vdash t:T$）

  则

  t 要么是一个值，要么对任何存储$\mu$ 使$\emptyset|\Sigma\vdash\mu$，存在某个项$t'$ 和存储$\mu'$，使得$t|\mu\rightarrow t'|\mu'$。

# 异常

# 提出异常

• 语法形式：

  $$t::=...|error$$

• 求值规则：

  $$error\;t_2\rightarrow error\\ v_1\;error\rightarrow error$$

• 类型规则：

  $$\Gamma\vdash error:T$$

  项$error$ 允许是任何类型，在任何上下文中出现。所以它破坏了类型的唯一性原理。

# 异常处理

• 语法形式：

  $$t::=...|try\;t\;with\;t$$

• 求值规则：

  $$try\;v_1\;with\;t_2\rightarrow v_1\\ try\;error\;with\;t_2\rightarrow t_2\\ \frac{t_1\rightarrow t_1'}{try\;t_1\;with\;t_2\rightarrow try\;t_1'\;with\;t_2}$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_1\quad\Gamma\vdash t_2:T}{\Gamma\vdash try\;t_1\;with\;t_2:T}$$

# 带值得异常

• 语法形式：

  $$t::=...|raise\;t|try\;t\;with\;t$$

• 求值规则：

  $$(raise\;v_1)\;t_2\rightarrow raise\;v_1\\ v_1\;(raise\;v_2)\rightarrow raise\;v_2\\ \frac{t_1\rightarrow t_1'}{raise\;t_1\rightarrow raise\;t_1'}\\ raise\;(raise\;v_1)\rightarrow raise\;v_1\\ try\;v_1\;with\;t_2\rightarrow v_1\\ try\;raise\;v_1\;with\;t_2\rightarrow t_2\;v_1\\ \frac{t_1\rightarrow t_1'}{try\;t_1\;with\;t_2\rightarrow try\;t_1'\;with\;t_2}$$

• 类型规则：

  $$\frac{\Gamma\vdash t_1:T_{exn}}{\Gamma\vdash raise\;t_1:T}\\ \frac{\Gamma\vdash t_1:T\quad\Gamma\vdash t_2:T_{exn}\rightarrow T}{\Gamma\vdash try\;t_1\;with\;t_2:T}$$

  其中，$T_{exn}$ 表示了可能出现的异常的种类。它可以是 Nat（对异常编码），或者 String 等。